Area and Midpoint Theorems

• Parallelograms on the same base and between the same parallels are equal in area.
• The area of a parallelogram is equal to the area of a rectangle on the same base and between the same parallels.
• Area of a triangle is half that of a parallelogram on the same base and between the same parallels.
• Triangles on the same base and between the same parallels are equal in area.
• The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
• The line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.

Exercise

1. In the following diagram, ABCD is a parallelogram. P and Q are points on the sides DC and BC respectively. Prove that
   (i) area of APB = area of AQD
   (ii) area of APB = area of ABQ +area of DQC.
                    
2. In the following figure, area of the parallelogram ABCD is 29 cm². If AB = 5.8 cm, find the height of the parallelogram EFCD.
3. In the following figure, AB || DC and area of ABD is 24 sq. units. If AB = 8 units, find the height of ABC.
                                   
4. In the following figure, AB || DC || EF, DA || EB and DE || AF. Prove that area of || gm DEFH = area of || gm ABCD.
   [Hint. Area of || gm ABCD = area of || ADEG = area of || gm DEFH.]
                                  
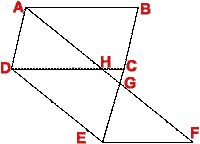
5. In the following figure, DE is parallel to the side BC of ABC. BE and CD intersect at O. Prove that
   (i) area of BED = area of CED.
   (ii) area of BOD = area of COE.
   (iii) area of ABE = area of ADC.
                                      
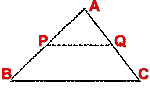
6. In ABC, P and Q are mid-points of the sides AB and AC respectively. If BC = 6 cm, AB = 5.4 cm and AC = 5 cm, calculate the perimeter of the quadrilateral PBCQ.
                                             
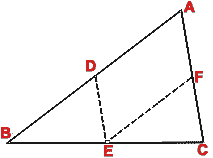
7. ABCD is a rectangle. E, F, G and H are the mid-points of the sides AB, BC, CD and DA respectively. Prove that EFGH is a rhombus.
   [Hint. EF is parallel and half of AC and HG is parallel and half of AC
     =>   EFGH is a || gm.
    Also FG = BD/2 but BD = AC   => FG = HG.]
                                          
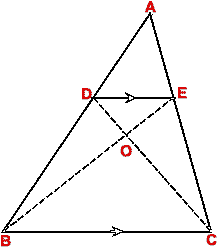
8. In ABC, D, E and F are the mid-points of the sides AB, BC and CA respectively. Prove that the S ADF, DBE, ECF and EFD are congruent to each other.
                             
9. In ABC, E and F are the mid-points of the sides BC and CA respectively. EF = 4 cm and ED || CA. If area of ||gm DEFA = 16 cm2, calculate.
   (i) AB      (ii) area of BED
   (iii) area of trapezium DECA.
   

Answers