Circles

• A circle is the set of all those points, say P, in a plane, each of which is at a constant distance from a fixed point in that plane.
• The fixed point is called the center and the constant distance is called the radius.
• All radii of a circle are equal.
                       
• A line segment joining any two points of a circle is called a chord of the circle.
• A chord of a circle passing through its center is called a diameter of the circle.
                        
• Length of diameter = 2 × radius
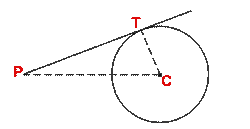
• A line which meets a circle in one and only one point is called a tangent to the circle.In the following figure, the line PT is a tangent to the circle with center C.
                         
• The point where the line meets (touches) the circle is called its point of contact. Notice that CP is perpendicular to PT.

Exercise

1. Fill in the blanks with correct word(s) to make the statement true:
   (i) Radius of a circle is one-half of its.....
   (ii) A radius of a circle is a line segment with one end point at..... and the other end on.....
   (iii) A chord of a circle is a line segment with its end points....
   (iv) A diameter of a circle is a chord that..... the center of the circle.
   (v) All radii of a circle are.....
2. State which of the following statements are true and which are false:
   (i) A line segment with its end-points lying on a circle is called a diameter of the circle.
   (ii) Diameter is the longest chord of the circle.
   (iii) The end-points of a diameter of a circle divide the circle into two parts; each part is called a semi-circle.
   (iv) A diameter of a circle divides the circular region into two parts; each part is called a semi-circular region.
   (v) The diameters of a circle are concurrent. The center of the circle is the point common to all diameters.
   (vi) Every circle has unique center and it lies inside the circle.
   (vii) Every circle has unique diameter.
   (viii) From a given point in the exterior of a circle two tangents can be drawn to it and these two tangents are equal in length.
3. Draw a circle with center O and radius 2.5 cm. Draw two radii OA and OB such that angle AOB = 60°. Measure the length of the chord AB.
4. Draw a circle of radius 3.2 cm. Draw a chord AB of this circle such that AB = 5 cm. Shade the minor segment of the circle.
   [Hint. To draw chord AB of length 5 cm, take a point A on the circle. With A as center and radius 5 cm, draw an arc to meet the circle at B. Join AB.]
5. Draw a circle of radius 4 cm with C as its center. Draw two radii CP and CQ such that PCQ = 45°. Shade the minor sector of the circle.
6. Find the length of the tangent drawn to a circle of radius 3 cm, from a point at a distance 5 cm from the center.
7. In the following figure, PT is a tangent to the circle with center C. Given CP = 20 cm and PT = 16 cm, find the radius of the circle.
                                 
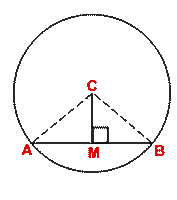
8. In the adjoining diagram, AB is a chord of a circle with center C. If CM is perpendicular to AB, prove that AM = MB. Hence complete the following statement: If a perpendicular is drawn from the center of a circle to a chord then it....the chord.
   [Hint.AMC CMB.]
                                               

Answers