Coordinate System
- When a horizontal number line and a vertical number line
are placed at right angles so that their origins coincide (the points corresponding to
zero), we get a Coordinate system or Coordinate plane.
- The horizontal line X' OX is called x-axis.
- The vertical line Y'OY is called y-axis.
- Their point of intersection is called origin.
- The points in the coordinate plane correspond to ordered pairs of real numbers.
Coordinates of a point
- Let P be any point in the coordinate plane. From P, draw PM perpendicular to X'OX. Then OM is called x-coordinate or abscissa
of P and is usually denoted by x. MP is called y-coordinate or ordinate of P and is usually denoted by y. We say
that point P corresponds to ordered pair (x, y), and we write P (x, y).
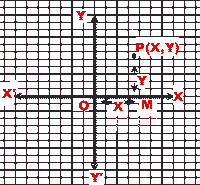
- Origin is the point (0, 0). Point (x, 0) lies on x-axis and point (0, y) lies on y-axis.
Quadrants
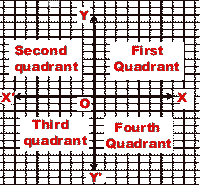
- The two axes divide the plane into four parts called quadrants.
- XOY' is called first quadrant. Here both x and y are positive.
- X'OY is called second quadrant. Here x is -ve and y is +ve.
- X'OY' is called third quadrant. Here both x and y are -ve.
- Y'OX is called fourth quadrant. Here x is +ve and y is -ve.
Exercise
- State whether true or false:
(i) Point (2, 0) lies on x-axis.
(ii) Point (-2, 0) lies on y-axis.
(iii) Point (0, y) lies on y-axis.
(iv) If point (x, y) lies on x-axis then abscissa is zero.
(v) If point (x, y) lies on x-axis then y = 0.
(vi) Point (-2, -3) lies in second quadrant.
- Plot the points A (1, 2), B (-4, 2), C (-4,
-1) and D (1, -1). What kind of quadrilateral is ABCD? Find its area.
- Plot the points A (2, 0), B (0, 5) and C (-2, 0). What kind of triangle is ABC? Find its area.
- Plot a rectangle which lies in first quadrant, has origin as one vertex, is 6 units long along
x-axis and 4 units long along y-axis. Give the coordinates of its vertices.
Answers
1. (i) T
(ii) F
(iii) T
(iv) F
(v) T
(vi)F
2. Rectangle; 15 square units
3. Isosceles triangle; 10 square units
4. (0, 0), (6, 0), (6, 4), (0, 4)


