Formulae

• Formula is an algebraic expression corresponding to a statement.
• The subject of a formula is a variable which is expressed in terms of the other variables involved in the formula. You also learnt how to change the subject of a formula.
• The method of finding the value of an algebraic expression by replacing all occurrences of variables with their particular values is called substitution.

Exercise

1. Write formulae for the following statements:
   (i) The length of a rectangle is 10 units more than breadth and the perimeter is 7 times the breadth.
   (ii) Anu is presently y years old. In 4 years time, she will be three times old as she was 2 years ago.
   (iii) If you multiply a number by 2 and take away 12, you get 2 more the number.
   (iv) A boy buys a number of pencils each costing Rs 2 and a number of erasers each costing Rs 3 and spends a total of Rs 26.
   (v) The circumference of a circle is times its diameter.
   (vi) A male daily wage labourer earns Rs 60 per day and a woman earns Rs 45 per day. Find the monthly earnings of x men and y women, assuming that there are 26 working days in a month.
2. Change the subject of each of the following formulae to the letter given against them
   (i) 9C + 160 = 5F; C
   (ii) 9C + 160 = 5F; F
   (iii) v² = u² + 2as; s
   (iv) v² = u² + 2as, u
   (v) s = ut + (1/2)at²; a
   (vi) m = n/(1 + n) ; n
   (vii) l = a + (n - 1) d; n
   (viii) (x + a)/(x + b) = c/d; x
   (ix) S =(n/2)[2a + (n - 1)d]; d
   (x) A = r²; r
   (xi) V = r² h; r
   (xii) V = r²h; h
3. When a = 2, b = 0 and c = - 3, find the value of
   (a) a³ + b³ + c³
   (b) (a + b + c)³
   (c) a² + b² + c² - 2ab - 2bc - 2ca
   (d) (a - b - c)².
4. Find the value of the polynomial x⁴ - x³ + 2x² - x + 5 when
   (a) x = 3
   (b) x = 0
   (c) x = - 3
5. When s = 3, t = 5, u = - 1, find the value of
   (a) stu + 3
   (b) s² + t² + u²
   (c) (s + t + u) stu
6. The area A of a circle is given by A = r² where = 22/7 and r is the radius.
   (i) Find A when r = 14 cms
   (ii) Find r when A = 99/14 cm².
7. If 9C + 160 = 5F, find
   (i) C when F = 50
   (ii) F when C = 50.
8. In the formula I = (P R T)/100, find R when I = 180, P = 2000, T = 9/2.

Answers

1. (i)7x = 2 (x + x + 10)    (ii) y + 4 = 3 (y - 2)
  (iii) 2x - 12 = x + 2         (iv) 2x + 3y = 26
   (v) C = D                  (vi) W = 26 (60x + 45y)
2. (i) C = (5/9)(F - 32)         (ii) F =(9/5)C + 32        (iii) s =(v² + u²)/2a
           (iv) u = ±(v² - 2as)         (v) a = 2(s - u t)/t²          (vi) n = m/(1 + m)
          (vii) n =(l - a + b)/d             (viii) x = (ad + bc)/(c - d)       (ix) d = 2 (S - an)/[n (n - 1)]
   (x) r = 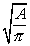                 (xi) r =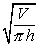
   (xii) h = V/ r²
3. (a) - 19               (b) - 1             (c) 29       (d) 25
4. (a) 74                 (b) 5              (c) 134
5. (a) - 12                (b) 35            ( c) - 105
6. (i) 616 cm²          (ii) 1.5 cm
7. (i) 10                   (ii) 122          8. 2