Fundamental Concepts and Operations of Algebra

• Product or quotient of a number of constants or variables is called a term. The terms having same literal factors are called like terms, otherwise they are called unlike terms.
• An algebraic expression or algebraic phrase is a collection of one or more terms separated by plus or minus signs. Monomials have one term, binomials have two terms, trinomials have three terms and polynomials have two or more than two terms.
• The degree of a polynomial in one variable x is the greatest of the powers of x present in the polynomial. The degree of a constant polynomial is zero.
• Addition, subtraction and multiplication of algebraic expressions can be done by using horizontal method or column method.
• The division of a polynomial by another can be checked by using the formula
      dividend = (divisor × quotient) +remainder
• Various grouping symbols are-, (), { } and [ ]. When removing the brackets, we start from innermost grouping symbol and work our way outwards.
• Rule of BODMAS is applicable in algebraic expressions also.

Exercise

1. Consider the algebraic expression (3/2)x²y -(1/2) xy² +6x²y². State whether the following statements are true or false.
   (i) It is a simple expression.
   (ii) It is a compound expression.
   (iii) It is a polynomial in two variables.
   (iv) It is a binomial.
   (v) The numerical coefficient of -x y²/2 is -1/2.
   (vi) The coefficient of x in term -x y²/2 is y².
2. Using column method, add ab+2bc-ca and 2ab-bc-ca and subtract 4ab+5bc-3ca.
3. Simplify
   (i) 2 (x -2y) -3 (x +2y +1) +5
   (ii) (2y -1)(3 -4y)
   (iii) (x +y +z)(x -y-z)
   (iv)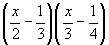
4. Multiply 1 -x +x² with 1 +x +x².
5. Simplify the expression
       2 (a² -b²) -[2a² -{b² -(a² +b² +ab)}].
   Find its value when a = 2 and b = -1.

Answers