Operations on Sets

• The union of sets A and B, written as AB, is the set consisting of all elements which belong to either A or B or both.
• If A is any set, then A = A, AA = A, A = .
• The intersection of sets A and B, written as AB is the set consisting of all the elements which belong to both A and B.
• If A is any set, then A = , AA = A, A = A.
• n(AB) = n(A) +n(B) -n(AB).
• If A and B are two sets, then difference of A and B is the set A -B consisting of all the elements which are elements of A but are not elements of B.
• Complement of a set A, written as A' or A^C is the set consisting of all the elements of which do not belong to A.
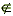  Thus A' = {x | x and xA}.
• If A is any set, then AA' = , AA' = , n(A) +n(A') = n().
• In Venn diagrams, sets are represented by closed figures like rectangle, circle, oval. Elements of the set are shown as points inside this figure. Usually the universal set is denoted by rectangle and its subsets by closed curves (circles etc.) within this rectangle.

Exercise

1. Let A = {-5, -3, 0, 3, 5}, B = { -4, -2, 0, 2, 4} and
   = { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}
   (i) Find AB
   (ii) Find AB
   (iii) Verify that n(AB) = n(A) +n(B) -n(AB)
   (iv) Find A'
   (v) Verify that n(A) +n(A') = n()
   (vi) Find B'
   (vii) Verify that n(B) +n(B') = n()
   (viii) Find AA' and AA'
   (ix) Find BB' and BB'
   (x) Find (AB)' and A'B'. Verify that they are equal.
   (xi) Find (AB)' and A'B'. Verify that they are equal.
   (xii) Find A -B and B -A. Are they equal?
2. Let A = {x | x is an even natural number less than 20} and
   B = {x| x is a multiple of 3 less than 20}
   Represent A and B by Venn diagrams. Hence find AB and AB.
3. Let A = {students who like cricket} and B = {students who like tennis}.
   Let n(A) = 20, n(B) = 15 and n(AB) = 5. Find n(AB).
4. Let n() = 50, n(A) = 15, n(B) = 13, n(AB) = 10.
   Find n(A'), n(B'), n(AB).
5. In a city, 50% people read newspaper A, 45% read newspaper B and 25% read neither A nor B. How many individuals read both the newspapers A as well as B?
6. Let = {triangles}, I = {isosceles triangles}, E = {equilateral triangles},
   R = {right angled triangles} and P = {obtuse angled triangles}.
   (i) Draw a Venn diagram to show these sets in their correct relationship.
   (ii) Shade the region representing IR and write the measures of the angles of the triangles of this region.
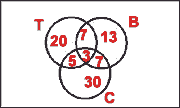
7. The students of a certain school have a choice of three games: Tennis, Badminton and Cricket. The following table gives the percentage of students who play some or all the games:

   Games	Tennis	Badminton	Tennis and Badminton	Badminton and Cricket	Cricket and Tennis	Cricket only	All Games
   % of students	35	30	10	10	8	30	3

   Draw a Venn diagram and use it to determine the percentage of students who
   (i) play Tennis only
   (ii) play Badminton only
   (iii) play Cricket
   (iv) do not play any of the games.

Answers

 1.(i) {-5, -4, -3, -2, 0, 2, 3, 4, 5}     (ii) {0}
    (iv) {-4, -2, -1, 1, 2, 4}                 (vi) {-5, -3, -1, 1, 3, 5}
    (viii) AA' = , A A' =              (ix) BB' = , BB' =
    (x) {-1, 1}                                      (x) {-5, -4, -3, -2, -1, 1, 2, 3, 4, 5}
    (xii) A -B = {-5, -3, 3, 5} and B -A = {-4, -2, 2, 4}. They are not equal.
2. A = {2, 4, 6, 8, 10, 12, 14, 16, 18} and B = {3, 6, 9, 12, 15, 18}.

                 
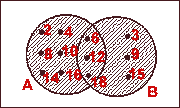
       AB = {2, 4, 6, 8, 10,12, 14, 16, 18, 3, 9, 15}    AB = {6, 12, 18}
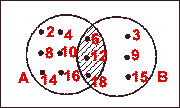
3.
     nbsp;nbsp;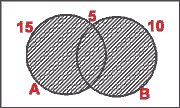  
        n(AB) = 15 +5 +10 = 30
4. n(A') = 35, n(B') = 37, n(AB) = 18
5. 20%
6. (i)
      
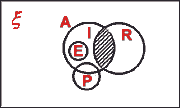
     (ii) 45°, 45°, 90°
7. (i) 20%        (ii) 13%           (iii) 45%             (iv) 15%.