Relations and Mappings

• Relation is an association between two objects.
• The concept of relation between two sets by finding the relation (rule of association) and drawing arrows from left hand side to right hand side.
• Mapping is an association between two sets A and B such that each element of A is associated with a unique element of B. So, "there must be an answer, and this answer should be unique".
• An ordered pair (a, b) is a pair of objects which occur in a particular order.
• Relations and mappings can also be represented by a set of ordered pairs and vice versa.
• Mappings are also called functions, usually denoted by letters f,g etc. The set of images is called range and the set of pre images is called domain of a function.
• A function may be written in roster form (set of ordered pairs) or as arrow diagram or in equation form (formula).

Exercise

1. Write true or false:
   (i) An ordered pair is a pair of objects taken in any order.
   (ii) (2, 3) = (3, 2)
   (iii) {2, 3} = (2, 3)
   (iv) If (x, 2) = (3, y) then x = 3, y = 2
   (v) If (x +1, y +1) = (5, 6) then x = 4, y = 5
   (vi) The relation {(0, 0), (0, 1), (0, 2)} is a mapping.
   (vii) The relation {(0, 0), (1, 0), (2, 0)} is a mapping.
   (viii) In a function each element has a unique image.
   (ix) Domain is the set of preimages.
   (x) Range is the set of images.
2. Consider R =
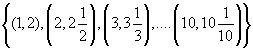
   (i) Is it a mapping? If yes, write it in equation form. Hence evaluate f(5).
   (ii) If f(x) = 37/6, find x.
   (iii) What is the domain?
   (iv) What is the range?
3. Consider the following arrow diagram:
       
   (i) Is it a function? Write it in equation form.
   (ii) List the elements of this function.
4. Given f : x 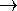1/x where x {integral multiples of 6}
   (i) What is the range of this function?
   (ii) Find f(18).
   (iii) If f(x) = 18, find x.
5. Consider the following diagram:
           
   (i) Is it a mapping? Write in roster form.
   (ii) Find the image of h.
   (iii) Find the preimage of 24.

Answers

1. (i) F         (ii) F          (iii) F       (iv) T       (v) T
   (vi) F       (vii) T        (viii) T     (ix) T       (x) T
2. (i) Yes; f(x) = x +1/x;  f(5) = 26/5
   (ii) f(x) = 37/6 = 6 +1/6, so x = 6
  (iii) Domain = {1, 2,.., 10}
  (iv) Range =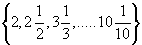
3. (i) Yes; f(x) = x³
   (ii) {(-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8)}.
4. (i) {even integers}
   (ii) 6                 (iii) 54
5. (i) Yes; {(a, 1), (b, 2),....., (y, 25), (z, 26)}
   (ii) 8                (iii) x