Triangles

• A triangle is a closed figure bounded by three line segments. It has three sides, three (interior) angles and three vertices.
                
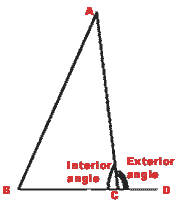
• The sum of an exterior angle and the adjacent interior angle is 180°.
• The sum of angles of a triangle is 180°.
• An exterior angle of a triangle is equal to the sum of its two opposite interior angles.
• In a triangle, the angles opposite equal sides are equal.
• In a triangle, the sides opposite equal angles are equal.
• In an equilateral triangle, each (interior) angle is 60°.
• The angles of an isosceles right angled triangle are 45°, 45° and 90°.
• Inequalities
  If two sides of a triangle are unequal, then the greater side has greater angle opposite to it.
  If two angles of a triangle are unequal, then the greater angle has greater side opposite to it.
  The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
  The difference between the lengths of any two sides of a triangle is less than the length of the third side.
• Tests for congruency of two triangles
  Two triangles are congruent if and only if they have exactly the same shape and the same size.
  S.A.S.-two sides and the included angle of one triangle are equal to two sides and the included angle of the other triangle.
  A.S.A.-two angles and the included side of one triangle are equal to two angles and the included side of the other triangle.
  A.A.S.-two angles and a (non-included) side of one triangle are equal to two angles and the corresponding side of the other triangle.
  S.S.S.-three sides of one triangle are equal to the three sides of the other triangle.
  R.H.S.-the hypotenuse and a side of one right angled triangle are equal to the hypotenuse and a side of the other right angled triangle.
• Pythagoras theorem
  In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
  If in a triangle the square on the longest side is equal to the sum of the squares on the other two sides, then the triangle is right angled and the angle opposite to the longest side is right angle.

Exercise

1. Calculate the value of x in each of the following sketches:
   (i)      (ii)
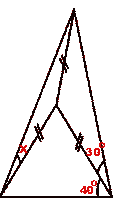
2. Calculate the size of each lettered angle in the following figures:
   (i) 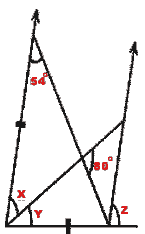         (ii)
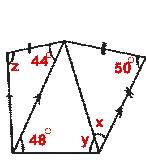
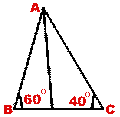
3. The vertical angle of an isosceles triangle is three times the sum of its base angles. Find all the angles of the triangle.
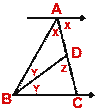
4. From the following diagram, prove that
   (i) x +y = 90°
   (ii) z = 90°
   (iii) AB = BC
                                           
5. PQR is a right angled triangle at Q and PQ:QR = 3:2. Which is the least angle?
6. In ABC, AB = 8 cm and BC = 6 cm. Find the greatest length and least length that CA can have.
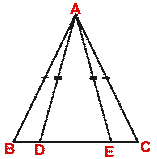
7. In the following figure, AD bisects A. Arrange AB, BD and DC in the ascending order of their lengths.
                                               
8. In the following figure, OA bisects A and ABO = OCA. Prove that OB = OC.
   [Hint. OAB OAC.]
                                              
9. In the following figure, AB = AC and AD = AE. Prove that BE = CD.
   [Hint. AB = AC => AD +DB = AE +EC
     => DB = EC, AD = AE
    Also AB = AC =>ABC = ACB.
    Prove that BCE BCD.]
                                                
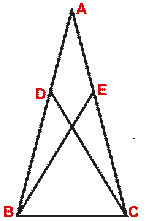
10. In the following figure, AB = AC and AD = AE. Prove that
    (i) ADB = AEC
    (ii) ABD AEC
    (iii) BE = DC.
    [Hint. (i) AD = AE =>ADE = AED
     Also ADB +ADE = 180°  = AED +AEC.]
                                                  
11. In the following diagram, ABCD and AEFG are squares. Prove that EB = GD.
    [Hint.DAG = 90° - GAB = BAE. and AEB AGD.]
                                                   
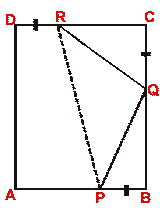
12. In the following figure, ABCD is a square and DR = CQ = BP. Prove that
    (i) RC = QB
    (ii) RQ = PQ
    (iii) PQR = 90°
    (iv) RPQ = 45°.
    [Hint. (ii) RQC PBQ.
              (iii) QPB +PQB +90° = 180°  =>QPB + PQB = 90°
              but QPB = RQC    => RQC +PQB = 90°.]
                                               
13. In the following figure, all measurements are in centimeters. Find the length of AD.                       
                                           
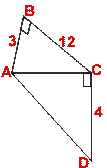
14. In the following figure, AB = 6 cm, BD = 3 cm and AD = BC. If ABC = 90°, find the length of AC.
                                                  
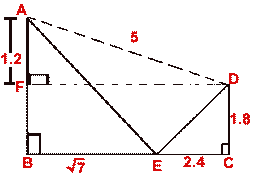
15. In the following figure, all measurements are in centimeters. Find
    (i) ED    (ii) AE
    Hence, prove that AE² +ED² = AD². State the size of AED.
                                      
16. One diagonal of a rhombus is 30 cm long. If one of its side is 17 cm, find the length of the other diagonal.

Answers