(i) Mean (for ungrouped data) =
(ii) Mean (for grouped data) =
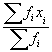 ,
where x1, x2, x3, ..., xn are
different variates with frequencies f1, f2, f3,
..., fn respectively.
,
where x1, x2, x3, ..., xn are
different variates with frequencies f1, f2, f3,
..., fn respectively.(iii) Mean for continuous distribution.
Let there be n continuous classes, yi be the class mark and fi be the frequency of the ith class, then
mean =
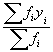 (Direct method)
(Direct method)Let A be the assumed mean, then
mean = A +
 ,
where di = yi -A (Short cut method)
,
where di = yi -A (Short cut method)If the classes are of equal size, say c, then
mean = A +c x
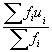 , where ui =
, where ui =
(i) Median is the central value (or middle observation) of a statistical data if it is arranged in ascending or descending order.
(ii) Let n be the total number of observations, then
| Median = |
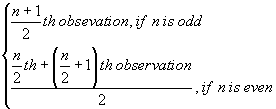 |
| (i) Lower Quartile = |
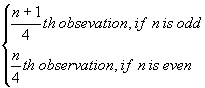 |
| (ii) Upper Quartile = |
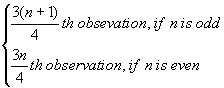 |
(iii) Inter quartile-range = upper quartile -lower quartile
(i) Mode (or modal value) of a statistical data is the variate which has the maximum frequency.
(ii) The class with maximum frequency is called the modal-class.