Circles
- The locus of a point which moves in a plane so that its distance from a fixed point in that plane
remains constant is called a circle. The fixed point is called the center and the constant distance
is called the radius.
- A line which meets a circle in one and only one point is called a tangent to the circle.
- Two circles are said to touch each other iff they have one and only one point in common.
- A common tangent to two circles is called a direct common tangent if both the circles lie on
the same side of it, and it is called a transverse (or indirect) common tangent if the circles lie on
opposite sides of it.
- Two or more circles are called equal (or congruent) iff they have same radius.
- Chord properties of a circle.
(i) The straight line drawn from the center of a circle to bisect a chord is perpendicular to
the chord, and conversely; the perpendicular to a chord from the center of the circle bisects the chord.
(ii) One and only one circle can be drawn passing through three non-collinear points.
(iii) Equal chords of a circle are equidistant from the center, and conversely; chords of a
circle that are equidistant from the center of the circle are equal.
- Angle properties of a circle.
(i) The angle subtended by an arc of a circle at the center is double the angle subtended
by it at any point on the remaining part of the circumference.
(ii) Angles in the same segment of a circle are equal.
(iii) Angle in a semi-circle is a right angle, and conversely; if an arc of a circle subtends a
right angle at any point on the remaining part of the circumference then the arc is a semi-circle.
(iv) The opposite angles of a cyclic quadrilateral are supplementary, and conversely; if a
pair of opposite angles of a quadrilateral are supplementary then the quadrilateral is cyclic.
(v) The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
- Arc properties of circles.
(i) Axiom of equal arcs. In equal circles (or in same circle), if two arcs subtend equal
angles at the centers (or center) then they are equal, and conversely; in equal circles
(or in same circle), if two arcs are equal then they subtend equal angles at the centers (or center).
(ii) In equal circles (or in same circle), equal chords cut off equal arcs, and conversely; in
equal circles (or in same circle), if two arcs are equal then their chords are equal.
- Tangent properties of circles.
(i) The tangent at any point of a circle and the radius through the point are perpendicular to each other.
(ii) If two tangents are drawn from an external point to a circle then
(1) the tangents are equal in length.
(2) the tangents subtend equal angles at the center of the circle.
(3) the tangents are equally inclined to the line joining the point and the center of the circle.
(iii) If two circles touch, then the point of contact lies on the straight line through their center.
(iv) Let r1, r2 be the radii of the bigger and smaller circles respectively,
and d be the distance between their centers then
(1) the circles touch externally iff r1 +r2 = d.
(2) the circles touch internally iff r1 -r2 = d.
(v) If a line touches a circle and from the point of contact, a chord is drawn, the angles between the tangent and the chord are
respectively equal to the angles in the corresponding alternate segments.
- Length of common tangent.
If r1, r2 are the radii of two circles and d is distance between their centers, then
(i) the length of a direct common tangent = 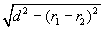
(ii) the length of a transverse common tangent = 
Exercise
- A chord of length 8 cm is drawn in a circle of radius 5 cm, find its distance from the center of circle.
- A chord of length 16 cm is at a distance 6 cm from the center of the circle. Find the length of the chord
of the same circle which is at a distance 8 cm from the center.
- In a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively.
Calculate the distance between the chords, if they are on
(i) the same side of the center.
(ii) the opposite sides of the center.
- AB and CD are two parallel chords of a circle. If AB = 6 cm, CD = 12 cm and distance between
these chords is 3 cm, find the radius of the circle.
- AB and CD are two parallel chords of a circle. If AB = 10 cm, CD = 24 cm and distance between
these chords is 17 cm, find the radius of the circle.
- In the following figure, the diameter CD of a circle is perpendicular to the chord AB.
If AB = 12 cm and CM = 2 cm, find the radius of the circle.
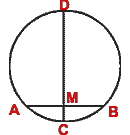
- AB is a diameter of a circle. C is a point in AB such that CA = 9 cm and CB = 25 cm.
Find the length of the shortest chord through C.
- The radii of two concentric circles are 17 cm and 10 cm. A line PQRS cuts the larger circle at P
and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
- The length of the common chord of two intersecting circles is 30 cm. If the radii of two circles
are 25 cm and 17 cm, find the distance between their centers.
- ABC is an isosceles triangle inscribed in a circle. If AB = AC = 12
 5 cm and BC = 24 cm, find the radius of the circle.
5 cm and BC = 24 cm, find the radius of the circle.
- (a) In the figure (i) given below, O is the center of the circle. If
 CBD = 56°, find
CBD = 56°, find
(i)  AEC
(ii)
AEC
(ii)  AOC.
AOC.
(b) In the figure (ii) given below, AC is a diameter of the circle. If BD = CD and
 APD = 69°, find
APD = 69°, find
 ACD.
ACD.
(i) 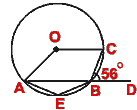 (ii)
(ii) 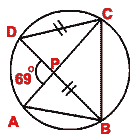
- (a) In the figure (i) given below, O is the center of the circle. If
 COD = 80°, find the values of x, y and z.
COD = 80°, find the values of x, y and z.
(b) In the figure (ii) given below, O is the center of the smaller circle, ABC and EDO are straight lines. If
 AED = 130°, find
AED = 130°, find
 COD.
COD.
(i) 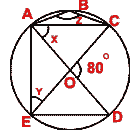 (ii)
(ii) 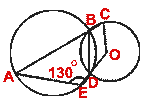
- (a) In the figure (i) given below, O is the center of the circle and
 AOC = 130°, find
AOC = 130°, find  ABC.
ABC.
(b) In the figure (ii) given below, AB is a diameter of the circle whose center is O. Given that  ECD =
ECD =
 EDC = 32°, calculate
(i)
EDC = 32°, calculate
(i)  CEF
(ii)
CEF
(ii)  COF.
COF.
(i) 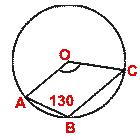 (ii)
(ii) 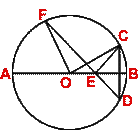
- (a) In the figure (i) given below, O is the center of the circle. Chords AB and CD meet at E. If
 CBE =
30° and
CBE =
30° and  CEA = 70°, find
CEA = 70°, find
 BOD.
BOD.
(b) In the figure (ii) given below, two chords AB and CD of a circle intersect at P. Prove that
AP.PB = CP.PD
[Hint.  APC ~
APC ~  DPB.]
DPB.]
(i) 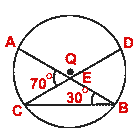 (ii)
(ii) 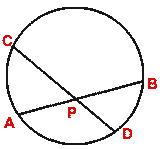
- (a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines,
 A = 35°,
A = 35°,
 Q = 25°. Find
(i)
Q = 25°. Find
(i)  PRB
(ii)
PRB
(ii)  PBR
(iii)
PBR
(iii)  BPR.
BPR.
(b) In the figure (ii) given below, O is the center of the circle. If chords AC and BD intersect at right
angles at E and  OAB = 35°, calculate
OAB = 35°, calculate  EBC.
EBC.
(i) 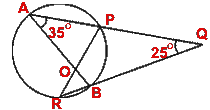 (ii)
(ii) 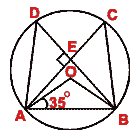
- Prove that angle subtended at the center of a circle is bisected by the radius passing through the mid-point of the arc.
- (a) In the figure (i) given below, two chords AB and CD of a circle intersect at P.
If AB = CD, prove that arc AD = arc CB.
(b) In the figure (ii) given below, AD is a diameter of the circle and chords AB, BC and CD are equal in
length. Given  DEF = 110°, calculate
(i)
DEF = 110°, calculate
(i)  AEF
(ii)
AEF
(ii)  BAF.
BAF.
(i) 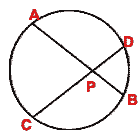 (ii)
(ii) 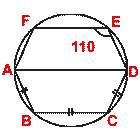
- (a) The figure (i) given below shows a pentagon, inscribed in a circle, center O.
Given AB = BC = CD and
 ABC = 132°. Calculate the value of
(i)
ABC = 132°. Calculate the value of
(i)  AEB
(ii)
AEB
(ii)  AED
(iii)
AED
(iii)  COD.
COD.
(b) In the figure (ii) given below, O is the center of the circle and AE is a diameter. If AB = BC and
 BFC = 25°, find the value of
(i)
BFC = 25°, find the value of
(i)  ABC
(ii)
ABC
(ii)  CDE.
CDE.
Prove that OB is parallel to EC.
(i)  (ii)
(ii) 
- (a) The figure (i) given below, AB and XY are diameters of a circle with center O. If
 APX = 30°, find
(i)
APX = 30°, find
(i)  AOX
(ii)
AOX
(ii)  APY
(iii)
APY
(iii)  BPY
(iv)
BPY
(iv)  OAX.
OAX.
Prove that arc AX = arc BY.
(b) In the figure (ii) given below, chord BC of the circle with center O is parallel to the radius OA.
The lines AC and OB meet at D. Prove that
(i)  ADB = 3
ADB = 3 ACB
(ii) AB = AX.
ACB
(ii) AB = AX.
(i) 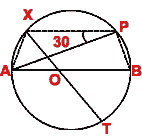 (ii)
(ii) 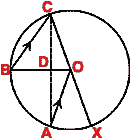
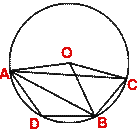
- In the figure below, A, D, B, C are four points on the circumference of a circle with center O.
Arc AB = 2 arc BC and
 AOB = 108°. Calculate in degrees
AOB = 108°. Calculate in degrees
(i) angle ACB (ii) angle CAB (iii) angle ADB.
Justify your calculations.
- A tangent to a circle of radius 3 cm from an external point P is of length 4 cm. Find the distance
of P from the nearest point of the circumference.
- Two concentric circles are of radii 17 cm and 15 cm. Find the length of the chord of the outer circle
which touches the inner circle.
- Two circles of radii 4 cm and 2·5 cm touch each other. Find the distance between their centers if they touch
(i) externally (ii) internally.
- (a) In the figure (i) given below, triangle ABC is circumscribed, find x.
(b) In the figure (ii) given below, quadrilateral ABCD is circumscribed and AD DC,
find x if radius of incircle is 10 cm.
DC,
find x if radius of incircle is 10 cm.
(i) 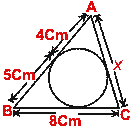 (ii)
(ii) 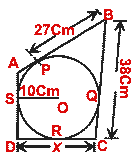
Answers
1. 3 cm
2. 12 cm
3. (i) 1 cm (ii) 7 cm
4. 3 5 cm
5. 13 cm
6. 10 cm
5 cm
5. 13 cm
6. 10 cm
7. 30 cm
8. 9 cm
9. 28 cm
10. 15 cm
11. (a) (i) 124° (ii) 112° (b) 23°
12. (a) x = 40°, y = 50°, z = 130° (b) 100°
13. (a) 115° (b) (i) 64° (ii) 64°.
14. (a) 80°
15. (a) (i) 35° (ii) 115° (iii) 30° (b) 35°
17. (b) (i) 20° (ii) 130°
18. (a) (i) 24° (ii) 48° (iii) 72°
(b) (i) 130° (ii) 140°
19. (a) (i) 60° (ii) 60° (iii) 30°
(iiv) 60°
20. (i) 54° (ii) 27°
(iii) 126°
21. 2 cm
22. 8 cm
23. (i) 6·5 cm (ii) 1·5 cm
24. (a) 7 cm (b) 21 cm

 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 

 (ii)
(ii) 