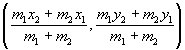Distance and Section Formulae
- Distance formula
The distance between the points P(x1, y1) and Q(x2,
y2) = 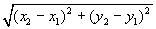
- Section formula
The co-ordinates of the point which divides (internally) the line segment
joining the points P(x1, y1) and Q(x2, y2)
in the ratio m1 : m2 are
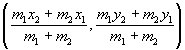
- Mid-point formula
The co-ordinates of the mid-point of the line segment joining the points P (x1,
y1) and Q2 (x2, y2) are

- Centroid formula
The co-ordinates of the centroid of a triangle whose vertices are A (x1,
y1), B (x2, y2) and C (x3, y3)
are 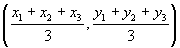
Exercise
- Calculate the distance between the points P(2, 2), Q(5, 4) correct to
three significant figures. (Do not consult tables).
- A is a point on the y-axis whose ordinate is 5 and B is the point (-3, 1).
Calculate the length of AB.
- The distance between A(1, 3) and B(x, 7) is 5. Find the possible values of x.
- P and Q have co-ordinates (-1, 2) and (6, 3) respectively. Reflect P in
the x-axis to P'. Find the length of the segment P'Q.
- Point A(2, -4) is reflected in the origin as A'. Point B(-3, 2) is
reflected in x-axis at B'. Write the co-ordinates of A' and B'. Calculate the
distance A'B' correct to one decimal place.
- The center of a circle of radius 13 units is the point (3, 6). P(7, 9) is
a point inside the circle. APB is a chord of the circle such that AP = PB.
Calculate the length of AB.
- A and B have co-ordinates (4, 3) and (0, 1) respectively. Find
(i) the image A' of A under reflection in the y-axis.
(ii) the image B' of B under reflection in the line AA'.
(iii) the length of A'B'.
- What point (or points) on the x-axis are at a distance of 5 units from the point (5, -4)?
- Find point (or points) which are at a distance of
 10 from the point (4, 3), given
that the ordinate of the point (or points) is twice the abscissa.
10 from the point (4, 3), given
that the ordinate of the point (or points) is twice the abscissa.
- Show that the points (3, 3), (9, 0) and (12, 21) are the vertices of a
right angled triangle.
- Show that the points (0, -1), (-2, 3), (6, 7) and (8, 3) are the vertices of a rectangle.
- The points A(0, 3), B(-2, a) and C(-1, 4) are the vertices of a right
angled triangle at A, find the value of a.
- Show by distance formula that the points (-1, -1), (2, 3) and (8, 11) are collinear.
- Calculate the co-ordinates of the point P that divides the line joining
the points A (-1, 3) and B(5, -6) internally in the ratio 1:2.
- Find the co-ordinates of the points of trisection of the line segment
joining the points (3, -3) and (6, 9).
- The line segment joining A(-3, 1) and B(5, -4) is a diameter of a circle
whose center is C. Find the co-ordinates of the point C.
- The mid-point of the line joining (a, 2) and (3, 6) is (2, b). Find the values of a and b.
- The mid-point of the line segment joining (2a, 4) and (-2, 3b) is (1, 2a
+1). Find the values of a and b.
- The center of a circle is (1, -2) and one end of a diameter is (-3, 2),
find the co-ordinates of the other end.
- Find the reflection of the point (5, -3) in the point (-1, 3).
Answers
1. 3·61 units
2. 5units
3. 4 or -2
4.  74 units
5. A'(-2, 4), B'(-3, -2); 6·1 units
74 units
5. A'(-2, 4), B'(-3, -2); 6·1 units
6. 24 units
7. (i) (-4, 3)
(ii) (0, 5)
(iii) 2 5 units
5 units
8. (2, 0) and (8, 0 .
9. (1, 2), (3, 6)
10. 67·5 sq. units
12. 1
14. (1, 0)
15. (4, 1), (5, 5)
16. (1,-3/2)
17. a = 1, b = 4
18. a = 2, b = 2
19. (5, -6)
20. (-7, 9)