Matrices
- Equal matrices
Two matrices A and B are called equal iff
(i) A, B are of the same order and (ii) their corresponding entries are equal.
If A = 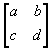 and B =
and B =  ,
then A = B iff a = p, b = q, c = r and d = s.
,
then A = B iff a = p, b = q, c = r and d = s.
- Addition of matrices
If A and B are two matrices of the same order then A +B is the matrix obtained
by adding the corresponding elements of A and B.
If A =  and B =
and B =  ,
then A +B =
,
then A +B = 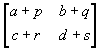
- Subtraction of matrices.
If A and B are two matrices of the same order then A -B is the matrix obtained
by subtracting the elements of B from the corresponding elements of A.
If A =  and B =
and B =  ,
then A -B =
,
then A -B = 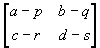
- Multiplication by a number
If k is any number and A is a matrix, then kA is a matrix
obtained by multiplying each element of the matrix A by k.
If A =  ,
then kA =
,
then kA = 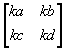 .
.
- Multiplication of two matrices.
Two matrices A and B are said to be conformable for the product AB iff
the number of columns in A is equal to the number of rows in B.
- If A is of order m × n and B is of order n × p,
then AB is of order m × p, and is defined as AB = [Cik]mxp
where (i, k) th element of AB = sum of the products of the
elements of the ith row of A with the corresponding element of the kth column
of B.
AB = 
Exercise
- Find the values of a, b, c and d if
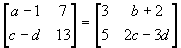
- Find the values of a and b if
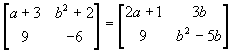
- If
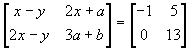 ,
find the values of x, y, a and b.
,
find the values of x, y, a and b.
- If
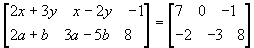 ,
find the values of x, y, a and b.
,
find the values of x, y, a and b.
- If A =
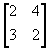 ,
B =
,
B =  and C =
and C = 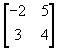 , find
, find
(i) A -B (ii) 3A -C (iii) AB (iv) BA (v) CB
- If A =
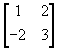 ,
B =
,
B = 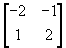 and C =
and C = 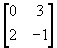 ,
find A +2B -3C.
,
find A +2B -3C.
- Let A =
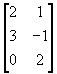 ,
B =
,
B = 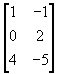 and C =
and C = 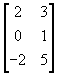 .
.
(i) Verify that (A +B) +C = A +(B +C).
(ii) Find 2A -3B +4C.
-
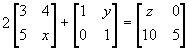 ,
find the values of x, y and z.
,
find the values of x, y and z.
- Find X if Y =
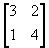 and 2X +Y =
and 2X +Y = 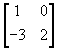 .
.
- Let A =
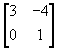 and B =
and B = 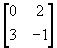 ,
find the matrix X if 2A +3X = 5B.
,
find the matrix X if 2A +3X = 5B.
- If A =
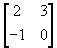 ,
B =
,
B = 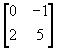 and C =
and C =  , verify that
, verify that
(i) (AB)C = A(BC)
(ii) A(B +C) = AB +AC
(iii) (A -B)C = AC -BC
- If A =
 ,
prove that (A -2I)(A -3I) = O where I is the unit matrix of order 2.
,
prove that (A -2I)(A -3I) = O where I is the unit matrix of order 2.
- If A =
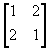 and B =
and B =  , find A (BA).
, find A (BA).
- If A =
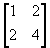 ,
B =
,
B = 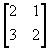 and C =
and C = 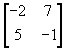 ,
show that AB = AC.
,
show that AB = AC.
- If A =
 ,
B =
,
B = 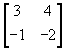 and C =
and C =  ,
find A(BC) and A(CB). Is A(BC) = A(CB)?
,
find A(BC) and A(CB). Is A(BC) = A(CB)?
- If A =
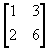 and B =
and B = 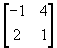 ,
does (A +B)² = A² +2 AB +B² hold?
,
does (A +B)² = A² +2 AB +B² hold?
- If A =
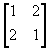 ,
show that A² -3I = 2A, where I is the unit matrix of order 2.
,
show that A² -3I = 2A, where I is the unit matrix of order 2.
- If
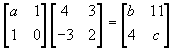 ,
find the values of a, b and c.
,
find the values of a, b and c.
- If A =
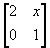 and B =
and B = 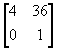 ,
find the value of x given that A² = B.
,
find the value of x given that A² = B.
- If A =
 ,
B =
,
B = 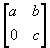 and AB = A +B, find the values of a, b and c.
and AB = A +B, find the values of a, b and c.
Answers
1. a = 4, b = 5, c = 2, d = -3
2. a = 2, b = 2
3. x = 1, y = 2, a = 3, b = 4
4. x = 2, y = 1, a = -1, b = 0
5. (i) 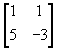 (ii)
(ii) 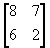 (iii)
(iii) 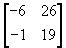
(iv)  (v)
(v) 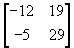
6. 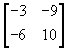 7. (ii)
7. (ii) 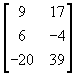
8. x = 2, y = -8, z = 7
9. 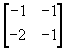
10. 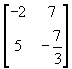 13.
13. 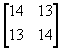
15. 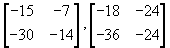 ;
A(BC)
;
A(BC)  A(CB)
16. No
A(CB)
16. No
18. a = 3, b = 9, c = 3
19. 12
20. a = 3/2, b = 0, c = 4/3
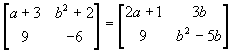
 ,
B =
,
B =  and C =
and C =  .
.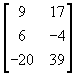
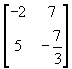 13.
13.