Mensuration
- Let h be the height and a be the side of an equilateral triangle, then h =
(
 3/2) a.
3/2) a.
- Circumference and area of a circle.
If r is the radius of a circle, then
(i) the circumference of the circle = 2 r
r
(ii) the area of the circle =  r²
r²
- Area of a circular ring.
If R and r are the radii of the bigger and smaller (concentric) circles, then
area of the ring =  (R² -r²).
(R² -r²).
- Circumference and area of a sector of a circle.
If r is the radius of the circle and the arc subtends an angle of n° at
the center, then
(i) the length of the arc = (n/360).2 r
= n
r
= n r/180
r/180
(ii) the area of the sector = (n/360). r²
r²
- Circumference and area of circumscribed and inscribed circles of an equilateral triangle.
If R and r are the radii of the circumscribed and inscribed circles of the triangle, then
(i) R = (2/3)h and r = (1/3)h
(ii) the circumference of the circumscribed circle = 2 R = (4/3)
R = (4/3) h
h
(iii) the area of the circumscribed circle =
 R² = (4/9)
R² = (4/9) h²
h²
(iv) the circumference of the inscribed circle = 2
 r = (2/3)
r = (2/3) h
h
(v) the area of the inscribed circle =  r² =
(1/9)
r² =
(1/9)  h²
h²
- Circumference and area of circumscribed and inscribed circles of a regular hexagon.
Let a be the side of a regular hexagon and R, r be the radii of the
circumscribed and inscribed circles respectively of the hexagon, then
(i) R = a and r = ( 3/2) a
3/2) a
(ii) the circumference of the circumscribed circle = 2 R
= 2
R
= 2 a
a
(iii) the area of the circumscribed circle =
 R² =
R² =
 a²
a²
(iv) the circumference of the inscribed circle = 2 r =
r =
 3
3  a
a
(iv) the area of the inscribed circle =  r²
= (3/4)
r²
= (3/4) a².
a².
Surface area and volume (of solids)
- Solid Cylinder.
Let r be the radius and h be height of a solid cylinder, then
(i) curved (lateral) surface area = 2  rh
rh
(ii) total surface area = 2  r(h +r)
r(h +r)
(iii) volume =  r²h
r²h
- Hollow cylinder.
Let R and r be the external and internal radii, and h be the height of a
hollow cylinder, then
(i) external curved surface area = 2 Rh
Rh
(ii) internal curved surface area = 2 rh
rh
(iii) total surface area = 2 (Rh +rh +R² -r²)
(Rh +rh +R² -r²)
(iv) volume of material =  (R² -r²)h
(R² -r²)h
- Cone.
Let r, h and l be the radius, height and slant height respectively of a cone, then
(i) slant height =  r² +h²
r² +h²
(ii) curved (lateral) surface area =  rl
rl
(iii) total surface area =  r(l +r)
r(l +r)
(iv) volume = (1/3)  r²h
r²h
- Solid sphere.
Let r be the radius of a solid sphere, then
(i) surface area = 4 r²
r²
(ii) volume = (4/3)  r³
r³
- Spherical shell.
Let R and r be the radii of the outer and inner spheres, then
(i) thickness of the shell = R -r
(ii) volume of material = (4/3)  (R³ -r³)
(R³ -r³)
- Solid hemisphere.
Let r be the radius of a hemisphere, then
(i) curved (lateral) surface area = 2 r²
r²
(ii) total surface area = 3 r²
r²
(iii) volume = (2/3)  r³
r³
- Hemispherical shell.
Let R and r be the radii of the outer and inner hemispheres, then
(i) the thickness of the shell = R -r
(ii) external curved surface area = 2  R²
R²
(iii) internal curved surface area = 2 r²
r²
(iv) total surface area =  (3R² +r²)
(3R² +r²)
(v) volume of material = (2/3) (R³ -r³)
(R³ -r³)
Exercise
- Find the length of the diameter of a circle whose circumference is 44 cm.
- Find the circumference of a circle whose area is 144
 cm².
cm².
- How many times will the wheel of a car rotate in a journey of 88 km if it
is known that the diameter of the wheel is 56 cm?
- (a) Calculate the radius of a cycle wheel in cm which makes 70 revolutions
in moving a distance of 154 m.
(b) A bucket is raised from a well by means of a rope which is wound round a
wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds
with a uniform speed of 1·1 m/s, calculate the number of complete revolutions
the wheel makes in raising the bucket. Take  to be 22/7.
to be 22/7.
- A road which is 7 m wide surrounds a circular park whose circumference is
352 m. Find the cost of paving the road at Rs 20 per m².
- The sum of radii of two circles is 7 cm and difference of their
circumferences is 8 cm. Find the circumferences of the two circles.
- Two circles touch externally. The sum of their areas is 58
 cm² and distance between their centers
is 10cm. Find the radii of the two circles.
cm² and distance between their centers
is 10cm. Find the radii of the two circles.
- The diameters of the two circles are in the ratio 3 : 4 and the sum of the
areas of the circles is equal to the area of a circle whose diameter is 36 cm.
Find the radii of the circles.
- A copper wire when bent in the form of an equilateral triangle has area
121
 3 cm². If the same wire is bent
into the form of a circle, find the area enclosed by the wire.
3 cm². If the same wire is bent
into the form of a circle, find the area enclosed by the wire.
- (a) In the figure (i) given below, ABCD is a square inscribed in a circle
of radius 7 cm. Calculate the area of the circle and the area of the shaded region.
(b) In the figure (ii) given below, ABCD is a rectangle with sides AB = 42 cm
and BC = 28 cm. Two quarter circles are drawn as shown in figure. Calculate
the area of the shaded part.
(i) 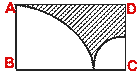 (ii)
(ii) 
- A rectangle with one side 4 cm is inscribed in a circle of radius 2·5 cm.
Find the area of the rectangle.
- (a) Find the area of the figure (i) given below in square cm correct to
one decimal place. (Take
 = 22/7)
= 22/7)
(b) The figure (ii) given below represents a quadrant of a circle of radius
3·5 cm, center O. Given OD = 2 cm, calculate the area of the shaded region.
(Take  = 22/7).
= 22/7).
(i)  (ii)
(ii) 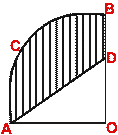
- (a) In the figure (i) given below, two circles with centers A and B touch
each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the
shaded region. (Take
 = 22/7).
= 22/7).
(b) In the figure (ii) given below, ABCD is a square of side 14 cm. A, B, C
and D are centers of circular arcs of radius 7 cm, find the area of the shaded
region. (Take  = 22/7).
= 22/7).
(i) 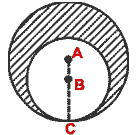 (ii)
(ii) 
- (a) The figure (i) given below represents a rectangular lawn 24 m by 18 m
with all the four corners rounded off by quarter circles of radii 3 m as
shown. Find the perimeter and the area of the lawn correct to 4 significant
figures. Take
 = 3·142.
= 3·142.
(b) The figure (ii) given below shows a running track which comprises of two
straight runs and semicircular tracks on the sides. AD = 21 m and DE = 3·5 m.
Find the difference in the distance run by an athlete, if he runs along the
outer edge or the inner edge.
(i) 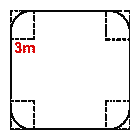 (ii)
(ii) 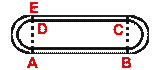
- (a) In the figure (i) given below, semi circles are described on the sides
of the right angled triangle PQR, right angled at P. If QR = 7 cm, calculate
the area of the shaded region.
(b) In the figure (ii) given below ABCD is a square inscribed in a circle.
With B and D as centers, quarter circles are drawn. If the side of the square
is 14 cm, find the area of the shaded region.
[Hint. Required area = area of circle with radius 7 2
cm -area of square ABCD +
2
cm -area of square ABCD +
2.(area of quarter circle with radius 14 cm -area of
 ABC).]
ABC).]
(i) 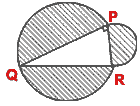 (ii)
(ii) 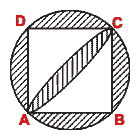
- (a) In the figure (i) given below, ABC is a right angled triangle,
 B = 90°, AB = 28 cm
and BC = 21 cm. With AC as diameter and with BC as radius a quarter circle is
drawn. Find the area of the shaded region correct to two decimal places. Take
B = 90°, AB = 28 cm
and BC = 21 cm. With AC as diameter and with BC as radius a quarter circle is
drawn. Find the area of the shaded region correct to two decimal places. Take
 to be 22/7.
to be 22/7.
(b) The boundary of the shaded region in the figure (ii) given below consists
of four semi-circular arcs, the smallest two being equal. If the diameter of
the larger is 14 cm and of the smallest is 3·5 cm, calculate the length of the
boundary and the area of the shaded region. (Take  = 22/7).
= 22/7).
(i) 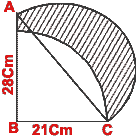 (ii)
(ii) 
- (a) In the figure (i) given below, the boundary of the shaded region
comprises of four semicircles and two quarter circles. If OA = OB = OC = OD =
7 cm and the straight lines AC, BD are perpendicular to each other, find the
length of the boundary and the area of the shaded region.
(b) In the figure (ii) given below, ABCD is a rectangle with sides AB = 19 cm
and BC = 12 cm. The arcs AP, PQ and QR are quadrants of circles. Find the area
of the shaded region and the length of the curved line.
(i) 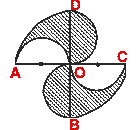 (ii)
(ii) 
- Find the radius of a circle if a 40° arc has length 4
 cm. Hence find the area of the sector formed by this arc.
cm. Hence find the area of the sector formed by this arc.
- (a) In the figure (i) given below, OABC is a sector of a circle of radius
6 cm. Calculate the perimeter and the area of the shaded region. Give your
answer correct to two decimal places.
(b) The figure (ii), represents the wiper of a car with the dimensions given
in the figure, find the area swept by the wiper and the perimeter of the
shaded area.
(i) 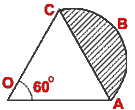 (ii)
(ii) 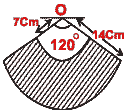
- A circle is inscribed in a regular hexagon of side 2
 3
cm. Find the circumference and the area of the inscribed circle.
3
cm. Find the circumference and the area of the inscribed circle.
- Find the total surface area of an open cylindrical vessel of length 42 cm,
and of external and internal diameters 20 cm and 6 cm respectively.
- An open cylindrical vessel is made of a metal. The internal diameter is 7
cm, the internal depth is 10 cm and the metal is 5 mm thick. Calculate the
capacity of the vessel and the volume of the metal.
- In the figure below, a rectangular platform is given with a semi-circular
end on one side. It is 23·5 m long from one end to the other. If the length of
half the circumference is 22 m, find the cost of constructing the platform 2·5
m high at the rate of Rs 6 per cubic meter.

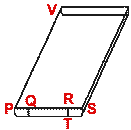
- The uniform cross-section PQRSTU of an open tank is formed of a
rectangular part QRTU and the two equal quarter circles PUQ and RTS. Given PS
= 1·6 m, UT = 72 cm and the length of the tank PV = 2 m, calculate the volume
of the water in cubic meters, which the tank can hold, when filled to
capacity. (Take
 = 22/7)
= 22/7)
- The total surface area of a right circular cone of slant height 13 cm is
90
 cm2. Calculate
cm2. Calculate
(i) its radius in cm. (ii) its volume in cm3.
Give your answer to (ii) in terms of  .
.
- A circus tent has lower part cylindrical and upper part of conical shape.
The radius of its base is 70 m. The total height of the tent is 30 m and that
of the cylindrical part is 6 m. Find the area of the canvas required to make the tent.
- The volume of a cone is the same as that of the cylinder whose height is 9
cm and diameter 40 cm. Find the radius of the base of the cone if its height is 108 cm.
- The entire surface of a solid cone of base radius 3 cm and height 4 cm is
equal to the entire surface of a solid right circular cylinder of diameter 4
cm. Find the ratio of (i) their curved surfaces. (ii) their volumes.
- A hollow metallic cylindrical tube has an internal radius of 3 cm and
height 21 cm. The thickness of the metal of the tube is 0·5 cm. The tube is
melted and cast into a right circular cone of height 7 cm. Find the radius of
the cone correct to one decimal place.
- A cone of maximum volume is carved out of a block of wood of size 20 cm x
10 cm x 10 cm. Find the volume of the cone carved out correct to one decimal
place. (Take
 = 3·1416).
= 3·1416).
- From a solid cylinder whose height is 8 cm and radius is 6 cm, a conical
cavity of height 8 cm and base radius 6 cm, is hollowed out. Find the volume
of the remaining solid correct to 4 significant figures. (
 = 3·1416).Also find the total surface area of the remaining solid.
= 3·1416).Also find the total surface area of the remaining solid.
- From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of
height 24 cm and of base radius 7 cm is drilled out. Find the volume and the
total surface of the remaining solid. (Take
 = 22/7).
= 22/7).
- An open cylindrical vessel of internal diameter 7 cm and height 8 cm
stands on a horizontal table. Inside this is placed a solid metallic right
circular cone, the diameter of whose base is 3·5 cm and height 8 cm. Find the
volume of the water required to fill the vessel. If the cone is replaced by
another cone, whose height is 1·75 cm and the radius of whose base is 2 cm,
find the drop in the water level.
- A solid cone of height 12 cm and base radius 6 cm has the top 4 cm removed
as shown in the adjoining below. Find the whole surface of the remaining solid.

- The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its
capacity in liters and the amount of sheet required to make this bucket. (Take
 = 22/7).
= 22/7).
Answers
1. 14 cm
2. 24  cm
3. 50000
4. (a) 35 cm (b) 40
cm
3. 50000
4. (a) 35 cm (b) 40
5. Rs 52360
6. 26 cm, 18 cm
7. 7 cm, 3 cm
8. 10·8 cm; 14·4 cm
9. 346·5 cm².
10. (a) 154 cm² (b) 56 cm² (b) 306 cm².
11. 12 cm²
12. (a) 115·3 cm (b) 6·125 cm².
13. (a) 122·57 cm² (b) 42 cm²
14. (a) 78·85 m; 424·3 m² (b) 22 m
15. (a) 38·5 m² (b) 224 cm²
16. (a) 428·75 cm² (b) 44 cm; 86·25 cm²
17. (a) (i) 66 cm (ii) 77 cm²
(b) (i) 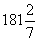 cm²
(ii)
cm²
(ii) 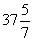 cm
cm
18. 18 cm; 36  cm²
cm²
19. (a) 12·28 cm; 3.27 cm² (b) (i) 154 cm² (ii) 58 cm
20. 6  cm 9
cm 9  cm²
cm²
21. 3718 cm².
22. (i) 385 cm³ (ii) 143 cm³
23. Rs 4620
24. 1·242 m³
25. (i) 5 cm (ii) 100 cm³
26. 18920 m²
27. 10 cm
28. (i) 15 : 16 (ii) 3 : 4
29. 5·4 cm
30. 1047·2 cm².
31. 603·2 cm²; 603·2 cm²
32. 3388 cm³; 2024 cm²
33. 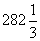 cm³;
cm³;
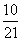 cm.
34. 350·66 cm²
cm.
34. 350·66 cm²
35. 20·02 litres; 3068 cm² (approximately)
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 
 (ii)
(ii) 


