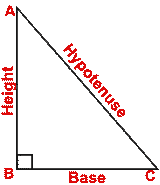
Pythagoras Theorem

• In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides. In the adjoining diagram, ABC is right angled at B.
  Pythagoras theorem states that AC² = AB² +BC²
          
• The converse of Pythagoras theorem is also true. If in a triangle, the square on one side is equal to the sum of squares on the other two sides, then the triangle is right angled at the angle contained by these two sides.

Exercise

1. Find the length of x in the following cases
   (i) (ii)
   (iii)
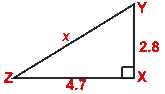
2. ABC is an isosceles triangle with AB = AC = 6 cm and BC = 8 cm. Find the length of the altitude on BC and hence calculate the area.
3. In ABC, AB = AC = x, BC = 5 cm and the area of the triangle ABC is 15 cm². Find x.
4. AD is perpendicular to the side BC of an equilateral triangle ABC. Prove that 4 AD² = 3 AB².
5. In an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that AD² = AC² +BD.DC
6. In ABC, B = 90° and M is a point on BC. Prove that AM² +BC² = AC² +BM².
7. In the following figure, D and E are mid-points of the sides BC and CA respectively of a ABC, right angled at C. Prove that
   (i) 4AD² = 4AC² +BC²
   (ii) 4BE² = 4BC² +AC²
   (iii) 4(AD² +BE²) = 5AB²
             
8. In the adjoining figure, ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-points of the sides AB and AC respectively. Calculate
   (i) the length of BC
   (ii) the area of ADE.
             
9. PQRS is a rhombus and the diagonals PR and SQ intersect at O. Prove that
    OP² +OR² = PS² +SR² -SQ²/2
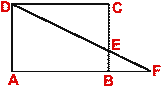
10. In the following diagram, ABCD is a rectangle, AB = 12 cm, BC = 8 cm and E is a point on BC such that CE = 5 cm. DE when produced meets AB produced at F.
    (i) Calculate the length DE.
    (ii) Prove that DEC ~ EBF and hence compute EF and BF.
                 
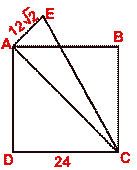
11. In the following figure, ABCD is a square of side 24 cm. Given EAC = 90° and AE = 122 cm.Calculate EC.
                     
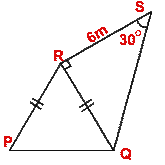
12. In the following figure, PQR is an isosceles triangle and RSQ is a right angled triangle. If RS = 6m and PQ = 4·6 m, find
    (i) RQ   (ii) the height of R above the ground.
               

Answers