Problems on Quadratic Equations

General suggestions for solving applied problems:

• Read Statement of the problem carefully and determine what quantity (or quantities) are needed.
• Represent the unknown quantity (or quantities) by a letter (or letters).
• Determine the expressions which are equal and write an equation (or equations).
• Solve the resulting equation (or equations).

Exercise

1. Find two positive consecutive numbers such that the sum of their squares is 85.
2. If the product of two positive consecutive odd integers is 195, find the integers.
3. The sum of two numbers is 18 and the sum of their squares is 170. Taking one number as x, form an equation and solve it to find the numbers.
4. The sum of the numerator and denominator of a certain positive fraction is 11. If 1 is added to both numerator and denominator, the fraction is increased by 3/56. Find the fraction.
5. Two squares have sides (x +6) cm and (2x +1) cm. The sum of their areas is 697 sq. cm. Express this as an algebraic expression and solve the equation to find the areas of the squares.
6. A rectangle of area 105 cm² has its length equal to x cm. Write its breadth in terms of x. If the perimeter is 44 cm, write an equation in x and solve it to find the dimensions of the rectangle.
7. The length of a rectangle is 3 cm more than its width. If the length is increased by 1 cm and the width is increased by 3 cm, the area is double the area of the original rectangle. Find the dimensions of the original rectangle.
8. A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 sq. meters, assuming the width of the walk to be x meters, form an equation in x and solve it to find the width of the walk.
9. The perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m. Find its area.
10. A 40 cm long wire is bent to form a right-angled triangle with hypotenuse 17 cm. Find the area of the triangle so formed.
11. In an auditorium, the number of rows was equal to the number of seats in each row. If the number of rows is increased by 6 and the number of seats in each row is increased by 2, then the total number of seats is increased by 172. How many rows were there?
12. An express train makes a run of 240 km at a certain speed. Another train, whose speed is 12 km/hr less, takes an hour longer to make the same trip. Find the speed of the express train.
13. A train covers a distance of 600 km at x km/hr. Had the speed been (x +20) km/hr, the time taken to cover the distance would have been reduced by 5 hours. Write down an equation in x and solve it to evaluate x.
14. An aeroplane flying with a wind of 30 km/hr takes 40 minutes less to fly 3600 km, than what it would have taken to fly against the same wind. Find the planes speed of flying in still air.
15. A swimming pool can be filled by 2 pipes together in 6 hours. If the larger pipe alone takes 5 hours less than the smaller pipe to fill the pool, find the time in which each pipe alone would fill the pool.
16. Three numbers are in the ratio 1/15:1/10:1/6. If the sum of their squares is 152, find the numbers.
17. When the cost price of an article is reduced by Rs 3, ten more articles can be bought for Rs 360. Find the original price of each article.
18. The hotel bill for a number of people for overnight stay is Rs 4800. If there were 4 more, the bill each person had to pay would have reduced by Rs 200. Find the number of people staying overnight.
19. A trader bought a number of articles for Rs 900. Five articles were damaged and he sold each of the rest at Rs 3 more than what he paid for it, thus getting a profit of Rs 150 on the whole transaction. Find the number of articles he bought.
20. Peter bought a watch for Rs 70x and sold it for Rs (750 +2x) at a profit of x%. Find the cost price of the watch.
21. A two digit number contains the bigger at unit place. The product of the digits is 24. If the difference between the digits is 5, find the number.
22. A year ago, father was 8 times as old as his son. Now his age is the square of his sons age. Find their present ages.
23. Two years ago, a mans age was three times the square of his sons age. In three years time, his age will be four times his sons age. Find their present ages.
24. The length (in cm) of the hypotenuse of a right-angled triangle exceeds the length of one side by 2 cm and exceeds twice the length of other side by 1 cm. Find the length of each side.
25. A speedboat travelled downstream at a distance of 10 km at an average speed of v km/hr. On the return journey, the average speed was increased by 5 km/hr and the journey took 6 minutes less. Find v.
26. An aeroplane travelled a distance of 400 km at an average speed of x km/hr. Write down an expression for the time taken. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time for the return journey. If the return journey took 30 minutes less than the outward journey, write down an equation in x and solve it.
27. A target on a dartboard has a center region of radius R cm and a concentric circle surrounding it of radius (R +1) cm. If the area between the two circles is one-tenth of the area of the center region, find R.

Answers

1. 6, 7                2. 13, 15           3. 7, 11         4. 4/7
5. (x +6)² +(2x +1)² = 697; 256 sq. cm, 441 sq. cm.
6. 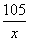cm; = 44; 15 cm, 7 cm
7. length = 7 cm, breadth = 4 cm
8. (16 + 2x)(10 +2x) -16.10 = 120; 2 m
9. 240 m².          10. 60 cm²          11. 20         12. 60 km/hr
13. 600/x - 600/(x+20)= 5; x = 40
14. 570 km/hr    15. 10 hours, 15 hours           16. 4, 6, 10
17. Rs 12           18. 8                   19. 7             20. Rs 700
21. 38                22. 7 years, 49 years               23. 5 years, 29 years
24. 15 cm, 8 cm, 17 cm                                     25. 20
26. 400/x hrs; 400/(x+40) hrs; 400/(x+40)= 400/x - 1/2; x =160
27. 20·5 cm approximately