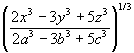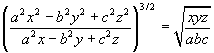Ratio and Proportion
- Compounded Ratio of two ratios a/b and c/d is ac/bd, i.e., ac : bd.
Duplicate ratio of a : b is a² : b²
Triplicate ratio of a : b is a³ : b³
Sub-duplicate ratio of a : b is  a :
a :  b
b
Sub-triplicate ratio of a : b is³ a :³
a :³ b
b
Reciprocal ratio of a : b is b : a
- Proportion. Four (non-zero) quantities of the same kind a, b, c, d are in proportion,
written as a : b :: c : d iff a/b = c/d
- The non-zero quantities of the same kind a, b, c, d, ... are in continued proportion iff
a/b = b/c = c/d = ...
In particular, a, b, c are in continued proportion iff a/b = c/d. In this case
b is called the mean proportion; b =  ac; c is called third
proportional. If a, b, c, d are in proportion, then d is called fourth proportional.
ac; c is called third
proportional. If a, b, c, d are in proportion, then d is called fourth proportional.
- Invertendo. If a : b :: c : d then b : a :: d : c
Alternendo. If a : b :: c : d then a : c :: b : d
Componendo. If a : b :: c : d then (a +b) : b :: (c +d) : d
Dividendo. If a : b :: c : d then (a -b) : b :: (c -d) : d
Componendo and dividendo.
If a : b :: c : d then (a +b) : (a -b) :: (c +d) : (c -d)
i.e., a/b = c/d => (a +b)/(a - b) = (c +d)/(c +d)
- If a/b = c/d = e/f = ..., then each ratio = (a +c +e +...)/(b +d +f +...)
Exercise
- Find the ratio of
(i) 45 minutes to 5¾ hours
(ii) 4 months and 2½ years
(iii) 1·2 kg and 60 gm.
- Find the compounded ratio of
(i) 5 : 7 and 9 : 10
(ii) (x +y) : (x -y) and (x -y) : (x +y)
(iii) 2a : 3b, 2b : 3a, a² : b²
- Find the following
(i) the duplicate ratio of 3 : 7
(ii) the triplicate ratio of 2 : 5
(iii) the sub-duplicate ratio of 36 : 25
(iv) the sub-triplicate ratio of 27 : 1
(v) the reciprocal ratio of 9 : 11.
- Find the following
(i) the duplicatae ratio of 2 x : 3
x : 3 y
y
(ii) the sub-duplicatae ratio of 16a² : 25b²
(iii) the sub-triplicate ratio of a6 : 8b³
- Which ratio is greater 17 : 21 or 23 : 28?
- Arrange the following ratios in descending order of magnitude
13 : 9, 25 : 23, 16 : 11 and 20 : 17
- Arrange the ratios 2 : 3, 3 : 4, 4 : 5 in ascending order of magnitude.
- A man earns Rs 5000 per month and spends Rs 3500 per month. Find the ratio of his
(i) expenditure to income
(ii) savings to income
(iii) savings to expenditure.
- If A : B = 4 : 5, B : C = 6 : 7, find A : C
- If A : B = 6 : 7, B : C = 8 : 9, find A : B : C
- Find the number which bears the same ratio to 7/33 that 8/21 bears to 4/9.
- Two numbers are in ratio 7 : 11. If 7 is added to each of the numbers,
the ratio becomes 2 : 3. Find the numbers.
- A ratio is equal to 3 : 7. If the antecedent is 5, find the consequent.
- Find two numbers in the ratio of 8 : 7 such that when each is decreased
by 12½, they are in ratio 11 : 9.
- Divide Rs 170 in the ratio 3 : 7.
- Find the value of x in the following proportions
(i) 10 : 35 = x : 42
(ii) 3 : x = 24 : 2
(iii) 2·5 : 11·5 = x : 3
(iv) x : 50 :: 3 : 2.
- Find the fourth proportional to
(i) 1/3, 1/4, 1/5
(ii) 1·5, 2·5, 4·5
(iii) 9·6 kg, 7·2 kg, 28·8 kg
(iv) 2xy, x², y²
- Find the third proportional to
(i) 5, 10
(ii) 1·3, 3·9
(iii) 21/4 and 7
(iv) x² -y², (x +y)²
(v) 2 x, 4 x².
- Find the mean proportion of
(i) 5 and 80
(ii) 1/12 and 1/75
(iii) 8·1 and 2·5
(iv)  5 +
5 + 2,
2,
 5 -
5 - 2
2
(v) (a -b)³, (a -b)5
- What should be subtracted from 23, 30, 57 and 78 so that the remainders may be in proportion?
- What number must be added to each of the numbers 6, 15, 20 and 43 to make them proportional?
- Find two numbers such that their mean proportional is 9 and the third proportional is 243.
- If three quantities are in continued proportion, prove that first is to
third is the duplicate ratio of the first to the second.
- If a
 b and a : b is the duplicate ratio of (a +c) and
(b +c), prove that c is the mean proportional between a and b.
b and a : b is the duplicate ratio of (a +c) and
(b +c), prove that c is the mean proportional between a and b.
- If b is the mean proportional between a and c, prove that
(a² -b² +c²)/(a-2 -b-2
+c-2) = b4
- If x/a = y/b = z/c, prove that each ratio is equal to
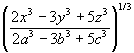
- If y is the mean proportional between x and z, prove that xyz(x +y +z)³ = (xy +yz +zx)³.
- If x/a = y/b = z/c, prove that
(i) 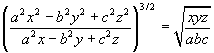
(ii) 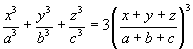
- If x/(b-c) = y/(c-a) = z/(a-b), prove that
(i) ax +by +cz = 0
(ii) x +y +z = 0
- If ax = by = cz, prove that x²/yz + y²/xz + z²/xy = bc/a² + ca/b² +ab/c²
- Find x from the following equations:
(i) [ (a +x) +
(a +x) + (a -x)]/[
(a -x)]/[ (a
+ x) -
(a
+ x) - (a - x)] = c/d
(a - x)] = c/d
(ii) 16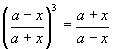
Answers
1. (i) 3 : 23
(ii) 2 : 15
(iii) 20 : 1
2. (i) 9 : 14
(ii) 1 : 1
(iii) 4a² : 9b²
3. (i) 9 : 49
(ii) 9 : 125
(iii) 6 : 5
iv) 3 : 1
(v) 11 : 9
4. (i) 4x : 9y
(ii) 4a : 5b
(iii) a² : 2b.
5. 23 : 28
6. 16 : 11, 13 : 9, 20 : 17, 25 : 23
7. 2 : 3, 3 : 4, 4 : 5
8. (i) 7 : 10
(ii) 3 : 10
(iii) 3 : 7
9. 24 : 25.
10. 48 : 56 : 63
11. 2/11
12. 49 and 77
13. 35/3
14. 40, 35
15. Rs 51, Rs 119
16 (i) 12
(ii) 1/4
(iii) 5
(iv) 75
17. (i) 3/20
(ii) 7·5
(iii) 21·6 kg
(iv) x y/2
18. (i) 20
(ii) 11·7
(iii) 28/3
(iv) (x +y)³/(x-y) (v) 8 x³
19. (i) 20 (ii) 1/30 (iii) 4·5
(iv)  3
(v) (a -b)4
3
(v) (a -b)4
20. 6
21. 3
22. 3,27
31. (i) 2acd/(c² +d²)
(ii) a/3