Relations and Functions
- A x B = {(a, b); for all a
 A, b
A, b  B}.
B}.
- If A and B are finite, then n(A x B) = n(A) x n(B).
- Let A, B be any two (non-empty) sets, then any subset of A
x B is called a relation from A to B. If R is a relation from A to B, then (a, b)
 R iff a R b.
R iff a R b.
- Domain of R = {x : x
 A, (x, y)
A, (x, y)  R for some y
R for some y
 B}, and range of R = {y : y
B}, and range of R = {y : y  B, (x, y)
B, (x, y)
 R for some x
R for some x  A}.
A}.
- R-1 = {(y, x) : y
 B, x
B, x  A, (x, y)
A, (x, y)
 R}.
R}.
- Let R be a relation on a set A, then
(i) R is reflexive iff a R a for all a  A.
A.
(ii) R is symmetric iff a R b implies b R a for all a, b  A.
A.
(iii) R is transitive iff a R b, b R c implies a R c for all a, b, c  A.
A.
(iv) R is equivalence iff R is reflexive, symmetric and transitive.
- A subset f of X x Y is called a function from X to Y iff
(i) for each x  X, there exists y
X, there exists y  Y such that (x, y)
Y such that (x, y)
 f, and
f, and
(ii) no two different ordered pairs have same first component.
- Range of f = {f (x): for all x
 X}.
X}.
- Let f be a function from X to Y then f is called
(i) one-one (or injection) iff different elements of X have different images in Y.
(ii) many-one iff two or more elements of X have same image in Y, i.e., f is not one-one.
(iii) onto (or surjection) iff each element of Y is the image of atleast one element of X,
i.e., iff range of f = Y.
(iv) into iff there exists atleast one element in Y which is not the image of any element
of X, i.e., iff range of f is a proper subset of Y.
(v) one-one correspondence (or bijection) iff f is both one-one and onto.
Exercise
- If the ordered pairs (x -2, y +1) and (3, x +7) are equal, find the values of x and y.
- If the ordered pairs (a, -1) and (5, b) belong to {(x, y) : y = 2x -3}, find the values of a and b.
- Find x and y if (x -1, y +3) = (y +4, 3x -6).
- If x
 {2, 3, 6} and y
{2, 3, 6} and y  {-4, 9, 10, 14}, form the set of all ordered pairs (x, y) such that x
is a factor of y.
{-4, 9, 10, 14}, form the set of all ordered pairs (x, y) such that x
is a factor of y.
- If x
 {4, 6, 7, 8} and y
{4, 6, 7, 8} and y  {6, 12, 20, 21, 28}, form the set of all ordered pairs (x, y) such
that x is a factor of y and x < y.
{6, 12, 20, 21, 28}, form the set of all ordered pairs (x, y) such
that x is a factor of y and x < y.
- Express {(x, y) : 2x +3y = 15, x, y
 W} as the set of ordered pairs.
W} as the set of ordered pairs.
- If A = {0, 1} and B = {2, 3, 4}, find
(i) A x B
(ii) B x A
(iii) A x A
(iv) B x B
Is A x B = B x A? Is n (A x B) = n (B x A)?
- If A = {3, 5} and B is an equivalent set obtained by trebling each element of A, find B x A.
- If A = {a : a
 W, a < 2} and B = {b : b
W, a < 2} and B = {b : b
 N, b
N, b  3}, find A x B and B x A.
Are A x B and B x A equivalent?
3}, find A x B and B x A.
Are A x B and B x A equivalent?
- A = {2, 3, 5} and some elements of A x B are (2, p), (3, q), (5, p). Find the set B and the remaining ordered pairs of A
x B such that order of A x B is least.
- If A and B are two sets, such that n(A) = 3 and n(B) = 2, find the number of relations
(i) from B to A (ii) on B (iii) on A.
- Let a relation R = {(2, -1), (3, 0), (5, 2) (4, 1), (6, 3)}
(i) write the domain and range of R.
(ii) write R in the builder form.
(iii) find R-1 in roster form.
(iv) represent R and R-1 by arrow diagrams.
- Let A = {3, 4, 7, 9}, B = {6, 7, 8, 9, 12} and R be the relation "is a factor of" from A to B.
Find R as a set of ordered pairs and find R-1.
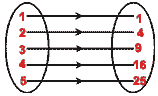
- The following arrow diagram represents a relation R. Represent the relation R in
(i) roster from
(ii) builder form.
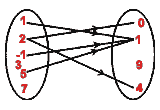
- (a) Write the relation represented by the following arrow diagram as a set of ordered pairs.
Also write the domain and the range of this relation.
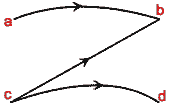
(b) Three arrows are missing from the following diagram which partly shows the relation "is greater than" on
the set of integers a, b, c and d. Copy and complete the diagram. State which is the smallest of the four integers.
- Let A = {2, 3, 6, 8} and B = {2, 3, 5, 7, 9}. Find (A
 B) x (A -B) and from this product pick out
the elements of the relation "is a factor of ".
B) x (A -B) and from this product pick out
the elements of the relation "is a factor of ".
- Find the linear relation between the components of the ordered pairs of the relation R
where R = {(3, 0), (0, -2), (6, 2), ...}.
- Copy and write "True" or "False" against each of the following statements:
(i) The relation "is greater than" in the set of integers is reflexive.
(ii) The relation "is similar to" in the set of triangles is transitive.
(iii) The relation "is perpendicular to" in the set of lines is transitive.
(iv) The relation "is a factor of" in the set of integers is symmetric.
- State whether the following relations on the given sets are equivalence relations or not:
(i) "is greater than" on W.
(ii) "is parallel to" on a set of lines.
(iii) "have same parents" on the set of people living in Calcutta.
(iv) "have equal perimeter" on a set of rectangles drawn in a plane.
- Let A be a set of triangles drawn in a plane, prove that the following relations on A are
equivalence relations:
(i) "is congruent to"
(ii) "is similar to"
(iii) "have equal area".
- Let I be the set of all integers, prove that the following relations on I are equivalence
relations:
(i) R = {(x, y) : x, y  I, x -y is even}
I, x -y is even}
(ii) R = {(x, y) : x, y  I, x -y is divisible by 5}.
I, x -y is divisible by 5}.
- A function f is defined by f(x) = x² +3, x
 N and x
N and x  5.
5.
(i) Find the range of f.
(ii) Find f(2). f(4)
(iii) Does f(6) exist?
(iv) Find x when f(x) = 7
(v) State whether the function is one-one or many-one.
- A function f on the set of real numbers R is defined as
f(x) = (3x+2)/(x -1). Find
(i) the domain of f
(ii) the range of f
(iii) the image of -2 under f (iv) x when f(x) = -3.
Answers
1. x = 5, y = 11
2. a = 1, b = 7
3. x = 2, y = -3
4. {(2, -4), (2, 10), (2, 14), (3, 9)}
5. {(4, 12), (4, 20), (4, 28), (6, 12), (7, 21), (7, 28)}
6. {(0, 5), (3, 3), (6, 1)}
7. (i) {(0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4)}
(ii) {(2, 0), (2, 1), (3, 0), (3, 1), (4, 0), (4, 1)}
(iii) {(0, 0), (0, 1), (1, 0), (1, 1)}
(iv) {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)}; No; Yes.
8. {(9, 3), (9, 5), (15, 3), (15, 5)}
9. A x B = {(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3)},
B x A = {(1, 0), (1, 1), (2, 0), (2, 1), (3, 0), (3, 1)}; Yes
10. B = {p, q}; (3, p), (2, q), (5, q)
11. (i) 64 (ii) 16 (iii) 512
12. (i) Domain of R = {2, 3, 4, 5, 6}, range of R = {-1, 0, 1, 2, 3}
(ii) R = {(x, y) : x  N, 1 < x < 7, y = x -3}
N, 1 < x < 7, y = x -3}
(iii) R-1 = {(-1, 2), (0, 3), (2, 5), (1, 4), (3, 6)}
(iv)
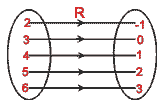
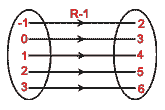
13. R = {(3, 6), (3, 9), (3, 12), (4, 8), (4, 12), (7, 7), (9, 9)};
R-1 = {(6, 3), (9, 3), (12, 3), (8, 4), (12, 4), (7, 7), (9, 9)}
14. (i) R = {(1, 1), (2, 4), (3, 9), (4, 16), (5, 25)}
(ii) R = {(x, y) : x  N,
x
N,
x  5, y =x²}
5, y =x²}
15.{(1,1), (2,0), (2,4), (-1,1), (5, 1)}
domain = { -1, 1, 2, 5} and range = {0, 1, 4}
16. {(2, 6), (2, 8), (3, 6), (3, 8)}; {(2, 6), (2, 8), (3, 6)}
17. 3y = 2x -6.
18. (i) False (ii) True (iii) False (iv) False
19. (i) No (ii) Yes (iii) Yes (iv) Yes
22. (i) {4, 7, 12, 19, 28} (ii) 133 (iii) No (iv) 2 (v) one-one
23. (i) 9 (ii) 9 (iii) 7, 6. No
24. (i) {-1, 0, 1, 2, 3, 4}
(ii) {(-1, -1), (0, 2), (1, 5), (2, -1), (3, -3), (3, -5)}
(iii) {-1, 2, 5, -3, -5} (iv) Many-one
25. (i) R except 1 (ii) R except 3
(iii) 4/3 (iv) 1/6




