Similarity

Two figures are called similar iff they have same shape, not necessarily the same size.
Axioms of similarity of triangles:
(i) A.A. (Angle -Angle) axiom of similarity.
(ii) S.A.S. (Side -Angle -Side) axiom of similarity.
(iii) S.S.S. (Side -Side -Side) axiom of similarity.
A line drawn parallel to one side of a triangle divides the other two sides in the same ratio, and conversely, if a straight line divides any two sides of a triangle in the same ratio, then the straight line is parallel to the third side of the triangle.

Exercise

(a) In the figure (i) given below, RQ || BC and PR || CA. If BP = 15 cm, PC = 20 cm, AQ = 16 cm and BR = 18 cm, calculate
(i) AR (ii) QC (iii) (RQ/BC).(AR/AB)
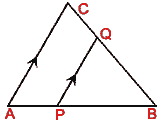
(b) In the figure (ii) given below (not drawn to scale), ABC is an isosceles triangle with AB = BC = 7·5 cm. If PQ || AC and AP:BP = 2:3, calculate
(i) CQ (ii) PQ (iii) area of trapezium APQC : area of PBQ.
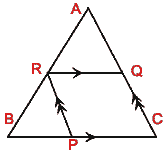(i) (ii)
(a) In the figure (i) given below, AP = 2PB and CP = 2PD.
    (i) Prove that ACP is similar to PBD and AC || BD.
    (ii) If AC = 4·5 cm, calculate the length of BD.
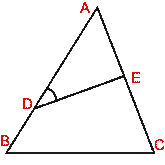
(b) In the figure (ii) given below, ADE = ACB.
    (i) Prove that s ABC and ADE are similar.
    (ii) If AE = 3 cm, BD = 1 cm and AB = 6 cm, calculate AC.
   (iii) Find area of ADE : area of ABC.
(c) In the figure (iii) given below (not drawn to scale), SP = 4 cm, SQ = 2 cm, PT = 3 cm and TR = 5 cm.
    (i) Prove that s PQR and PST are similar.
    (ii) Calculate ST if QR = 5·4 cm.
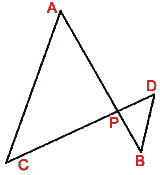(i) (ii)
(iii)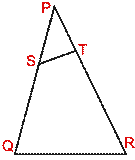
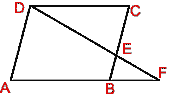
(a) In the figure (i) given below, PQ || SR, PT = 4 cm, TR = 3 cm and QS = 10 cm, compute QT and TS.
(b) In the figure (ii) given below, ABCD is a parallelogram. E is a point on BC such that BE = 2 cm. The straight line DE meets AB produced at F. If BF = 4 cm and AB = 6 cm, find the perimeter of the parallelogram ABCD.
(i) (ii)
If AD and BE are medians of ABC and through D a straight line is drawn parallel to BE to meet AC at F, prove that
(i) EF = FC (ii) AG : GD = 2 : 1
(a) In the figure (i) given below, B = P and PAB = QAC
    (i) Prove that s ABC and APQ are similar.
    (ii) Prove that s APB and AQC are similar.
    (iii) Given AP = (2/3)AB and QC = 3 cm, find the length BP.
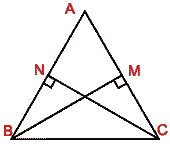
(b) In the figure (ii) given below, BM and CN are altitudes of ABC. Prove that
    (i) AB/AC = BM/CN = AM/AN                      (ii) (BN/MC).(HN/MH) = BH²/CH²
(c) In the figure (iii) given below, ACP = ABC. If AC = 9 cm, PC = 12 cm and BC = 15 cm, calculate
    (i) AB          (ii) AP              (iii) BN : PM.
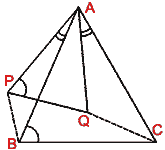(i) (ii)
(iii)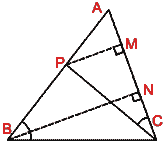
In a ABC, DE || BC. If AD = (4x-3) cm, DB = (3x -1) cm, AE = (8x -7) cm and EC = (5x-3) cm, find the value of x.
(a) In the figure (i) given below, BA, FE and CD are parallel lines. Given that AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate (i) EF (ii) AC.
(b) In the figure (ii) given below, AF, BE and CD are parallel lines. Given that AF = 7·5 cm, CD = 4·5 cm, ED = 3 cm, BE = x and AE = y. Find the values of x and y.
(i) 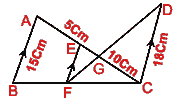(ii)
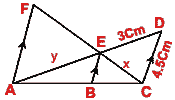
(a) In the figure (i) given below, AB || DC, ABC = CAD = 90°. If AC = 5 cm and AB = 4 cm, find CD and AD.
(b) In the figure (ii) given below, AB || DC. If AB = 4 cm, DC = 6 cm, PC = PD = 4·5 cm, find
(i) AP (ii) DP : DB (iii) AD : BC.
(c) In the figure (iii) given below, AB || DC and AB = 2DC. If AD = 3 cm, BC = 4 cm and AD, BC produced meet at E, find
(i) ED (ii) BE (iii) area of EDC : area of trapezium ABCD.
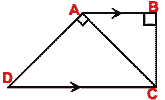(i) (ii)
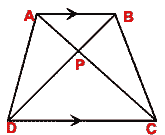
(iii)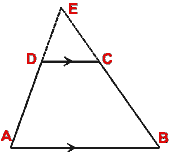
Prove that the diagonals of a trapezium divide each other proportionally.
If the diagonals of a quadrilateral divide each other proportionally, prove that it is trapezium.
The perimeters of two similar triangles are 40 cm and 25 cm. If a side of the first triangle is 16 cm, find the length of the corresponding side of the second triangle.
The scale of a map is 1 : 200000. A plot of land of area 20 km² is to be represented on the map. Find
(i) The number of kilometers on the ground which is represented by 1 cm on the map.
(ii) The area in km2 that can be represented by 1 cm².
(iii) The area on the map that represents the plot of land.

Answers

1. (a) (i) 24 cm (ii) 12 cm (iii) 16/49 (b) (i) 3 cm (ii) 4·5 cm (iii) 16 : 9
2. (a) (ii) 2·25 cm (b) (ii) 10 cm (iii) 1 : 4 (c) (ii) 2·7 cm
3. (a)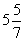

cm;

cm   (b) 22 cm
5. (a) (iii) 2 cm   (c) (i) 11·25 cm (ii) 7·2 cm    (iii) 16 : 25
6. 1                    7. (a) (i) 9 cm    (ii) 25 cm    (b)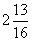

cm; 5 cm
8. (a) 6¼ cm; 3¼ cm (b) (i) 3 cm (ii) 3 : 5 (iii) 1 : 1
(c) (i) 3 cm (ii) 8 cm (iii) 1 : 3
11. 10 cm 12. (i) 2 km (ii) 4 km² (iii) 5 cm²