Hence (A +2 a)/(A -b) + (A +2 b)/(A -a)
=
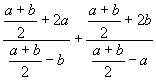
= (5a + b)/(a - b) + (5b + a)/(b - a) = (4a - 4b)/(a-b)
= 4
Insert six arithmetic means between 2 and 16. Also prove that their sum is 6 times the A.M. between 2 and 16.
Let A1, A2, ..., A6 be six A.M.s between 2
and 16. Then, by def., 2, A1, A2, ..., A6, 16
are in A.P.
Let d be the common difference. Here 16 is the 8th term.
16 = 2 +7d => d = 2.
Hence six A.M.s are a +d, a +2d, ..., a +6d
i.e. 4, 6, 8, 10, 12, 14.
Now sum of these means
= 6(4 +14)/2 = 54 = 6.9 = 6(2 +16)/2
= 6 times the A.M. between 2 and 16.
If A is the A.M. between a and b, show that
(A +2 a)/(A -b) + (A +2 b)/(A -a) = 4
Since A is the A.M. between a and b, A = (a +b)/2
Hence (A +2 a)/(A -b) + (A +2 b)/(A -a)
=
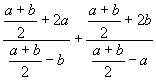
= (5a + b)/(a - b) + (5b + a)/(b - a) = (4a - 4b)/(a-b)
= 4