Angle

• If rotation is anticlockwise, the angle is positive. If rotation is clockwise, the angle is negative. One full rotation indicates 360°.
• An angle is said to be acute angle if 0° < 90°;
  right angle if = 90°; obtuse angle if 90° < < 180°;
  a straight angle if = 180°; and
  a reflex angle if 180° < < 360°.

There are three systems of measurement of an angle:

1. Sexagesimal system
   In this system an angle is measured in degrees, minutes and seconds. A complete rotation describes 360°.
   1 right angle = 90° (Since right angle is 1/4 th of full rotation)
   A degree is further subdivided as
   1degree = 60 minutes, written as 60'
   and 1 minute = 60 seconds, written as 60''.
   Thus 30·25° = 30° 15', 1·5' = 1' 30'' etc.
   We say that 30·25° is in degrees notation; 30° 15' is in degree-minute-second notation.
2. Centesimal system
   In this system an angle is measured in grades, minutes and seconds.
   Here 1 right angle = 100 grades, written as 100g.
   1 grade = 100 minutes, written as 100` and
   1 minute = 100 seconds, written as 100``.
   Thus 30·25g = 30g25`, 1·5` = 1`50`` etc.

Circular system

In this system an angle is measured in radians. The circular measure of an angle is the number of radians it contains.
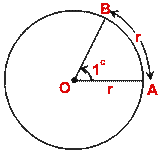
A radian is an angle subtended at the center of a circle by an arc whose length is equal to the radius. A radian is a constant angle.

Conversion Formula

       radians = 2 right angles = 180° = 200 g.

Length of an arc of a circle

If an arc of length s subtends an angle radians at the center of a circle of radius r,
then s = r

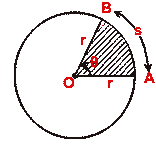
Area of a sector of a circle

Area of sector = (1/2)r² = (1/2) s

Illustrative Examples

Example

Express in degrees, radians as well as in grades the fourth angle of a quadrilateral, which has three angles 46° 30' 10'', 75° 44' 45'', 123° 9' 35'' respectively. (Take = 355/113)

Solution

The sum of three given angles
           = 46° 30' 10'' +75° 44' 45''+123° 9' 35''
           = 245° 24' 30'' (since 90'' =1'30'' and 84' =1°24')
The sum of all four angles of quadrilateral = 360°.
Fourth angle = 360° -(245° 24' 30'') = 114° 35' 30''
                                      (since 360° = 359° 59' 60'')
To convert it into radians,
    114° 35' 30'' = 114° +(35 + 30/60)'
         = 114°(71/2)' = 114° +(71/120)°
         = (13751/120)°
         = (13751/120) x (/180) radians        (As 180° = radians)
          = (13751/120) x (1/180) x (355/113) = 2 radians nearly
To convert the angle into centesimal system,
(13751/120)° = (13751/120) x (100/90) grades (since 90° = 100 grades)
   = 127·3241 grades = 127g 32` 41``.

Example

If G, D, denote respectively, the number of grades, degrees and radians in an angle, prove that

1. G/100 = D/90 = 2 /
2. G -D = 20 /

Solution

We know that 1 right angle = 100g = 90° = /2 radians.
Let the angle be X right angles.
Then G = 100 X, D = 90 X, = (/2) X         ...(1)

1. From (1), X = G/100 = D/90 = 2 /
   Hence the result.
2. From (1), G -D = 100 X -90 X = 10 X
                            = 10 x 2 / = 20 /

Exercise

1. Draw diagrams for the following angles:
   (i) -135° (ii) 740°. In which quadrant do they lie?
   (iii) Find another positive angle whose initial and final positions are same as that of -135°, and indicate on the same diagram.
2. If lies in second quadrant, in which quadrant the following will lie?
   (i) /2     (ii) 2       (iii) - .
3. Express the following angles in radian measure as well as centesimal measure:
   (i) 45°     (ii) 40° 37' 30''.
4. The circular measure of an angle is 1·5. Express it in English as well as French system. Take = 3·14.
5. The wheel of a carriage is 91 cms in diameter and makes 5 revolutions per second. How fast is the carriage running?
6. A wheel makes 180 revolutions in a minute. Through how many radians does it turn in one second?
7. Large hand of a clock is 21 cm long. How much distance does its extremity move in 20 minutes?
8. Find the angle between the hands of a clock at 7.20 P.M.
9. Sum of two angles is 80 grades and difference is 18°. Find the angles in degrees.
10. The difference between two acute angles of a right-angled triangle is /3 in circular measure. Find these angles in degrees.
11. The circular measures of two angles of a triangle are 1/2 and 1/3. Find the third angle in English system.
12. The difference of two angles is 1° while their sum is 1 in circular measure. Find the angles in degrees in terms of .
13. The angles of a triangle are in A.P. and the greatest is double the least. Find all the angles in circular system.
14. Express the angle 236·345° in
    (i>) degree-minute-second notation  (ii) radians.

Answers

1. (i) Third quadrant    (ii) First quadrant    (iii) 225°
2. (i) First quadrant    (ii) Third or fourth quadrant
  (iii) Third quadrant
3. (i) /4 radians; 50 grades
   (ii) 65 /228 radians; 45 g 13` 89``
4. 85° 59' 14'' or 95g 54` 14``
5. 51· 48 km / hour            6. 6
7. 44 cm                            8. 100°
9. 45° and 27°                   10. 63°, 27°
11. 132° 16' 22''
12. (180 +)/2 , (180 +)/2
13. 2/9, /3, 4/9  radians
14. (i) 236° 20' 42''  (ii) 4·125 radians