Locus / Regions in Argand Plane
Since any complex number z = x +iy corresponds to point (x,y) in complex plane
(also called Argand plane), so many kinds of regions and geometric figures in this plane
can be represented by complex equations or inequations.
The equation of circle of radius r and center at origin is |z| = r.
Note that for the circle |z -z0| = r,
all points on the circumference are given
by |z -z0| = r,
all points within the circle are given by |z -z0| < r,
while all points outside the circle are given by |z -z0| > r.
Illustrative Examples
Example
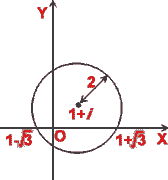
What is the equation of the circle in complex plane with radius 2 and center
at 1 +i? Does the origin lie within this circle, on the circle or outside it?
Does any real number lie on this circle?
Solution
Here center z0 = 1 +i, radius = 2.
So the equation of the circle is |z -z0| = r,
that is, |z -(1+i)| = 2
Now, the distance of origin from center
 (0 -1)
² +(0 -1)² =
(0 -1)
² +(0 -1)² =  2 < radius 2.
2 < radius 2.
Thus the origin lies within the circle.
Now let the real number (a,0) lie on the circle.
So  (a -1)² +(0 -1)² = 2
(a -1)² +(0 -1)² = 2
=> (a -1)² +1 = 4
=> (a -1)² = 3
=> a -1 = ± 3
3
=> a = 1 ± 3
3
Now you try to find out if any purely imaginary number lies on this circle.
Example
(i) Interpret the loci arg z =  /4 in complex plane.
/4 in complex plane.
(ii) Interpret the loci arg (z -1) =  /4 in complex plane.
/4 in complex plane.
(iii) Represent |z +i| = |z -2| in Argand plane.
(iv) How would you represent the line x -y = 0 in terms of complex number z?
Solution
(i) arg (z) =  /4 represents a half ray as shown in the following diagram.
/4 represents a half ray as shown in the following diagram.
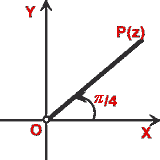
Note that the point z = 0 is not included as arg z is not defined for z = 0.
(ii) arg (z -1) =  /4 represents a half ray as shown in following diagram.
/4 represents a half ray as shown in following diagram.
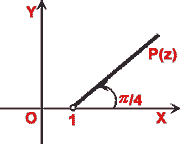
Note that the point z = 1 is not included.
(iii) Let z = x +iy, then
|z +i| = |z -2|
=> |x +iy +i| = |x +iy -2|
=> |x +(y +1)i| = |(x -2) +iy|
=> x² +(y +1)² = (x -2)² + y²
=> 4x +2y = 3, which represents a line in Argand plane
Note that intuitively, |z +i| = |z -2| represents all points equidistant from -i and 2 i.e. it represents
the perpendicular bisector of join of -i and 2.
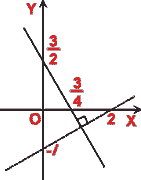
(iv) The line x -y = 0 is shown in the following diagram.
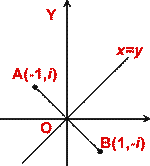
We note taht the points A(-1,i) and B(1,-i) are such that the line x -y = 0 is perpendicular bisector of AB.
Hence required equation in terms of z is
|z -(-1 +i)| = |z -(1 -i)|
i.e. |z +1 -i| = |z -1 +i |.
Exercise
- Write the equation or inequalities for the following:
(i) a circle of radius 2 with center at origin.
(ii) all points lying outside the circle of radius  2 and center at -1 -i.
2 and center at -1 -i.
(iii) a circle with center at 1 +i and passing through origin.
(iv) all points lying in first or fourth quadrant.
(v) the y-axis.
(vi) all points lying in first quadrant.
- Which regions are given by following? Also indicate on complex plane.
(i) 2  |z|
|z|  3
3
(ii) |z -2 -3i| > 2
(iii) Re(z) > 2
(iv) Re(1/z) < 1/2
(v) arg(z -1 -i) =  /4
/4
(vi) |z -1| +|z +1| = 3
(vii) |z -1|² +|z +1|² = 4
(viii) |z +i| 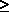 |z +2|
|z +2|
(ix) |z -2i| = |z +2i|
- Find the locus of a complex number z = x +iy satisfying the
relation |z +i| = |z +2|. Illustrate the locus of z in the Argand plane.
- Given z1 = 1 +2i. Determine the region in the complex plane represented
by 1 < |z -z1|
 3. Represent it with the help of an Argand diagram.
3. Represent it with the help of an Argand diagram.
- Find the locus of a complex number z = x +iy satisfying the relation
arg(z -a) =
 /4, a
/4, a R.
Illustrate the locus of z in Argand diagram.
R.
Illustrate the locus of z in Argand diagram.
- Find the locus of a complex number z = x +iy satisfying the relation
 .
Illustrate the locus of z in the Argand diagram.
.
Illustrate the locus of z in the Argand diagram.
Answers
1. (i) |z| = 2
(ii) |z +1 +i|> 2
2
(iii) |z -1 -i| =  2
[ Hint. radius = distance between origin and 1 +i.]
2
[ Hint. radius = distance between origin and 1 +i.]
(iv) Re(z)> 0
(v) Re(z) = 0
(vi) Re(z)> 0 and Im(z)> 0
2. (i) it represents circular annulus lying between concentric circles of radii 2 and 3 centered at
origin. All points on circumference of two circles are included. (You draw the diagram!)
(ii) all points lying outside circle of radius 2 centered at 2 +3i.
(iii) all points to the right of line x = 2.
(iv) exterior of a circle of radius 1 with center (1,0).
(v) portion of a line of inclination 45° passing through point 1 +i of the line x-y = 0.
(vi) an ellipse with foci at (1,0) and (-1,0), and major axis of length 3.
(vii) a circle with points (-1,0), (1,0) as end points of a diameter; in other words, a circle of radius 1 centered at
origin.
(viii) all points to the "left" of the line 4x-2y+3=0.
(ix) The x-axis.
3. The line 4x-2y+3=0, it is the perpendicular bisector of the join of the points -i and -2. (Please draw the diagram!)
4. It represents circular annulus lying between concentric circles of radius 1 and 3 centered at (1,2).
The region includes all points on the circumference of the outer
circle but excludes all point on the circumference of the inner circle. (You draw the diagram!)
5. It represents a portion of the line x-y-a=0. (Please draw the diagram!)
6. It represents the circle x² +y² +12 y +4
= 0 with center at (0,-6) and radius = 4 2 units.
2 units.


![]() (0 -1)
² +(0 -1)² =
(0 -1)
² +(0 -1)² = ![]() 2 < radius 2.
2 < radius 2.![]() (a -1)² +(0 -1)² = 2
(a -1)² +(0 -1)² = 2![]() 3
3![]() 3
3![]() /4 in complex plane.
/4 in complex plane.![]() /4 in complex plane.
/4 in complex plane.![]() /4 represents a half ray as shown in the following diagram.
/4 represents a half ray as shown in the following diagram.
![]() /4 represents a half ray as shown in following diagram.
/4 represents a half ray as shown in following diagram.

