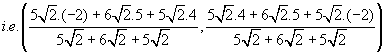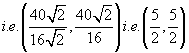Centroid and Incenter

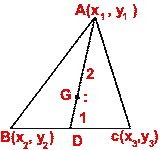
The point which divides a median of a triangle in the ratio 2 : 1 is called the centroid of the triangle. Thus, if AD is a median of the triangle ABC and G is its centroid, then
      AG/GD = 2/1
         

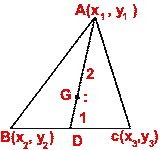
By section formula, the co-ordinates of G are
       
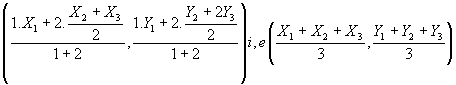
The symmetry of the co-ordinates of G shows that it also lies on the medians through B and C. Hence the medians of a triangle are concurrent.

Incenter of a triangle

The point of the intersection of any two internal bisectors of the angles of a triangle is called the incenter of the triangle. It is usually denoted by I.
         
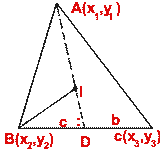
If the internal bisector of A of a ABC meets the side BC in D, then
        BD/DC = AB/AC
By section formula, the co-ordinates of I are

The symmetry of the co-ordinates of I shows that it also lies on the internal bisector of C. Hence the internal bisectors of the angles of a triangle are concurrent.

Illustrative Examples

Example

Find the co-ordinates of the incenter of the triangle whose vertices are(-2,4), (5,5) and (4,-2).

Solution

Let A (-2,4), B (5,5) and C (4,-2) be the vertices of the given triangle ABC, then
a = | BC| = [(4 -5)² +(-2 -5)²] =[1 +49] = 50 = 52,
b = |CA| = [(4 -2)² +(-2 -4)²] = [36 +36] = 72 = 62 and
c = |AB| = [(5 -2)² +(5 -4)²]   = [49 +1] = 50 = 52.
The co-ordinates of the incenter of ABC are
          
     
      

Exercise

1. Find the centroid of the triangle whose vertices are (-1,4), (2,7) and (-4,-3).
2. Find the point of intersection of the medians of the triangle whose vertices are (3,-5), (-7,4) and (10,-2). [Hint. Find centroid.]
3. Find the third vertex of a triangle if two of its vertices are (3,-5) and (-7,4), and the medians meet at (2,-1).
4. Find the centroid of the triangle ABC whose vertices are A(9,2), B(1,10) and C(-7,-6). Find the co-ordinates of the middle points of its sides and hence find the centroid of the triangle formed by joining these middle points. Do the two triangles have same centroid?
5. If (-1,5), (2,3) and (-7,9) are the middle points of the sides of a triangle, find the co-ordinates of the centroid of the triangle.
6. If A(1, 5), B (-2,1) and C(4,1) are the vertices of ABC, and internal bisector of A meets side BC at D, find |AD|. Also find the incenter of ABC.
7. Find the co-ordinates of the center of the circle inscribed in a triangle whose angular points are (-36,7), (20,7) and (0,-8).

Answers