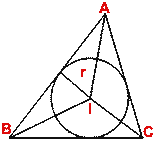
Circles connected with a given Triangle
The circle which passes through three vertices of a triangle is called the
circumscribing circle or circumcircle.
The center of this circle is called circumcenter, usually denoted as
O, and its radius is called circumradius, usually denoted as R. It can
be shown that circumcenter is the point of intersection of right bisectors of
the sides of a triangle.
The (unique) circle which is drawn within a triangle so as the three sides
touch this circle is called the inscribed circle or incircle.
The center of this circle is called incenter, usually denoted by I, and
its radius is called inradius, usually denoted by r. It can be shown
that incenter is the point of concurrence of the bisectors of the three
(internal) angles of the triangle.
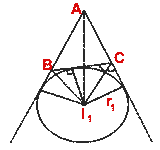
The circle which lies outside the triangle and touches the side BC and also
the sides AB and AC produced is called escribed circle or excircle
opposite to angle A. Its center is called excenter and its radius is
called exradius. It can be shown that excenter is the point of
concurrence of internal bisector of angle A and external bisectors of angles B
and C. Similarly there are two more excircles, one opposite to angle B and one
opposite to angle C. The three excenters are usually denoted as I1,
I2, I3 and the three ex-radii are usually denoted as r1,
r2, r3.

The Circumradius
In any  ABC,
ABC,
- R = a/(2 sin A) = b/(2 sin B) = c/(2 sin C), and
- R = abc/4

The Inradius
In any  ABC,
ABC,
- r =
 /s
/s
- r = (s -a) tan A/2 = (s -b) tan B/2 = (s -c) tan C/2
-
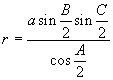
The Exradius
In any  ABC,
ABC,
- r1 =
 /(s-a) = s tan A/2 = (s -c) cot B/2 =
(s -b) cot C/2
/(s-a) = s tan A/2 = (s -c) cot B/2 =
(s -b) cot C/2
-
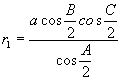
Illustrative Examples
Example
In any  ABC, prove that
ABC, prove that
1/r1 +1/r2 +1/r3 = 1/r
Solution

= (3s - 2s)/  = s/
= s/ = 1/r
= 1/r
Example
In a  ABC, a = 18, b = 24, c = 30 cms. Find:
ABC, a = 18, b = 24, c = 30 cms. Find:

- R
- r
- r1, r2 , r3
- Area of circumcircle
- Area of incircle
- Area of escribed circle opposite angle B
Solution
2s = a +b +c = 18 +24 +30 = 72 cm => s = 36 cm
 =
=  [s (s -a)(s -b)(s -c)] =
[s (s -a)(s -b)(s -c)] =
 [36.18.12.6] = 216 cm²
[36.18.12.6] = 216 cm²- R = abc/4
 = (18.24.30)/(4.216) = 15 cm
= (18.24.30)/(4.216) = 15 cm
- r =
 /s = 216/36 = 6 cm
/s = 216/36 = 6 cm
- r1 =
 /(s-a) = 216/18 = 12 cm,
/(s-a) = 216/18 = 12 cm,
r2 =  /(s-b) = 216/12 = 18 cm,
/(s-b) = 216/12 = 18 cm,
r3 =  /(s-c) = 216/6 = 36 cm
/(s-c) = 216/6 = 36 cm
- Area of circumcircle = R² =
 (15)² = 225
(15)² = 225
 cm²
cm²
- Area of incircle =
 r² =
r² =
 (6)² = 36
(6)² = 36 cm²
cm²
- Area of escribed circle opposite to angle B
= r2² =
(18)² = 344 cm²
Exercise
In a  ABC, prove the following (1 -9):
ABC, prove the following (1 -9):
- s = 4 R cos A/2 cos B/2 cos C/2
 = 2R² sin A sin B sin C
= 2R² sin A sin B sin C- (a +b) sec [(A-B)/2] = 4R cos C/2
- R(a² +b² +c²) = abc(cot A +cot B +cot C)
- (s/a -1)(s/b -1)(s/c -1) = r/R
- (b +c) tan A/2 +(c +a) tan B/2 + (a +b) tan C/2 = 4(R +r)
- 8Rr(cos²A/2 +cos²B/2 +cos²C/2) = 2(ab +bc +ca)-(a² +b² +c²)
- (i) r r1 r2 r3 =
 ²
²
(ii) (r1 -r) (r2 -r) (r3 -r) = 4 R² r
(iii) rr1/(r2r3) = tan² A/2
- (r1 +r2)(r2 +r3)(r3
+ r1) = 4 R s²
- If r1 = r2 +r3 +r, prove that A = 90°
- If a² +b² +c² = 8 R², prove that the triangle is right angled.
- If the diameter of an excircle is equal to the perimeter of the triangle,
show that the triangle is right angled.
- If in a
 ABC, a = 4 cm, b = 5 cm, c = 6 cm, calculate
ABC, a = 4 cm, b = 5 cm, c = 6 cm, calculate
(i) (ii) R
(iii) r (iv) r1, r2,
r3
(ii) R
(iii) r (iv) r1, r2,
r3
(v) lengths of altitudes p1, p2, p3
(vi) area of circumcircle (correct upto 2 decimals. Use
 = 22/7)
= 22/7)
(vii) area of incircle
(viii) area of escribed circle opposite to angle C
(ix) length of bisector of angle A
(x) sin A
(xi) sin A/2
- If in a
 ABC, a : b : c = 5 : 6 : 7, find the ratio of
the radius of the circumcircle to that of incircle.
ABC, a : b : c = 5 : 6 : 7, find the ratio of
the radius of the circumcircle to that of incircle.
- If the area of a triangle is 24 sq. cm. and its ex-radii are 4 cm, 1 cm,
12 cm, find the lengths of its three sides.
- If the angles of a triangle are in ratio 1 : 2 : 3 and its circumradius
is 10 cm, show that the lengths of its sides are 10 cm, 20 cm,
10
 3 cm.
3 cm.
Answers
13. (i) 9·921 sq. cm
(ii) 3· 024 cm
(iii) 1·323 cm
(iv) 2·83, 3·97, 6·61 cm
(v) 5·67, 7·94, 13·23 cm
(vi) 28·74 cm²
(vii) 5·50 cm²
(viii) 137·32 cm²
(ix) 5·102 cm
(x) 0·66
(xi) 0·353
14. 35 : 16
15. 6, 8, 10 cm






![]() ABC,
ABC,![]() ABC,
ABC,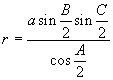
![]() ABC,
ABC,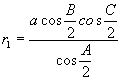
![]() ABC, prove that
ABC, prove that![]()
![]() = s/
= s/![]() = 1/r
= 1/r![]() ABC, a = 18, b = 24, c = 30 cms. Find:
ABC, a = 18, b = 24, c = 30 cms. Find:![]() ABC, prove the following (1 -9):
ABC, prove the following (1 -9):