Representations of Complex Numbers

Geometric representation

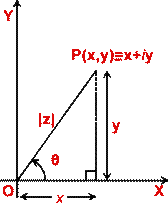
The complex number z = x +iy can be uniquely represented by the point P(x, y) in the co-ordinate plane and conversely corresponding to the point P(x, y) in the plane there exists a unique complex number z = x +iy. The plane is called the complex plane and the representation of complex numbers as points in the plane is called Argand diagram.

Notice that length OP = x² +y² = |z|
Also note that every real number x = x +0i is represented by point (x, 0) lying on x-axis, and every purely imaginary number iy is represented by point (0, y) lying on y-axis. Consequently, x-axis is called the real axis and y-axis is called the imaginary axis.

• If z₁ = x₁ +iy₁ and z₂ = x₂ +iy₂ are two complex numbers, then the distance between two corresponding points P₁(x₁, y₁) and P₂(x₂, y ₂) is
  |P₁P₂| = [(x₁ -x₂)² +(y₁ -y₂)²] = |z₁ -z₂| = |z₂ -z₁|.
• If P₁(x₁, y₁) and P₂(x ₂, y₂) are two points, then the point Q dividing [P₁P₂] in the ratio m : n is given
  Putting m = n = 1, the mid-point of z₁ and z₂ =

Trigonometric representation

z = x +iy = r cos +i r sin   = r (cos +i sin )
This form of z is called trigonometric form or polar form. Thus if modulus of z is r and amp(z) = , then z = r (cos +i sin ) = r cis .
Notice that if x = 0, then = /2; if y > 0 and = - /2 if y < 0.
If x 0, then tan = r sin /r cos = y/x, so that
     amp (z) = = tan^-1(y/x)
The unique value of q such that - < is called principal value of amplitude or argument.

For example, let z = 1 +i. Then
r = [(1)² + (1)²] = 2 and = tan^-1 1 = /4.
As another example, let r = 2 , = - /4
Then z = r (cos +i sin )
  
 

Remark

Frequently we have to convert the complex number z = x +i y to its polar form z = r cis . Do the calculations as follows:
    r = x² +y²
To find :
If x = 0 i.e. if z is purely imaginary, then
             = /2 if y> 0, = -/2 if y < 0.
If y = 0 i.e. if z is purely real, then
            = 0 if x > 0, = if x < 0.
Otherwise, let be such that 0 < < /2
Then = if x > 0, y > 0 (i.e. z is in first quadrant)
        = - if x < 0, y > 0 (i.e. z is in second quadrant)
        = + if x < 0, y < 0 (i.e. z is in third quadrant)
        = - if x>0, y<0 (i.e. z is in fourth quadrant).
Conversely, given z = r cis , convert it to standard form z = x +iy by using x = r cos , y = r sin .

Illustrative Examples

Example

If z is any complex number, show that -|z|Re(z)|z|. When do the equality signs hold?

Solution

Let z = x +iy = r cis = r (cos +i sin ) where r = |z| 0 and = amp(z).
We know that -1 cos 1 for all
=> -r r cos r          (as r0)
=> -|z| Re(z) |z|.      (because Re(z) = r cos )
Now -|z| = Re(z)  <=>     -[x²+y²] = x     <=>    y = 0 and x 0.
Also Re(z) = |z|    <=>      x = [x²+y²]      <=>    y = 0 and x 0.
Hence -|z| = Re(z) = |z|     <=> y = 0 and x = 0 => z = 0.

Example

Show that the area of the triangle on the Argand plane formed by the complex numbers z, iz and z +iz is |z|²/2

Solution

Note that the points O(0), P(z), R(z +iz) and Q(iz) form parallelogram OPRQ.
Also |OP| = |z| = |iz| = |OQ| and POQ = 90°
Thus 0, z, z +iz, iz form a square of side |z|.
Hence area of triangle with vertices z, iz and z +iz
   = (1/2)|z|.|z| = (1/2)|z|²

Exercise

1. Represent the following complex numbers in polar form
   (i) 3 +i
   (ii)
   (iii) sin 90° +cos 90°
   (iv) tan -i
   (v) 1 +sin +i cos
   (vi) -1 -i
2. Represent the following complex numbers in standard form x +iy
   (i) cis 2/3
   (ii)
3. If z is a complex number, represent -z and -iz in complex plane.
4. Using distance formula, prove that the points 1, (-1 +3i)/2 and (-1 -3i)/2 form the vertices of an equilateral triangle in complex plane.
5. Using distance formula or otherwise, prove that the points -2 +3i, -1 +2i and 2 +5i are collinear.
   [Hint. Let the points A, B, C represent the complex numbers -2 +3i,-1 +2i and 2 +5i respectively. Show that AB +BC = AC.]
6. If z₁, z₂, z₃, z₄ are complex numbers, show that they are vertices of a parallelogram in the Argand diagram if and only if z₁ +z₃ = z₂ +z₄.
   [Hint. What is mid-point of AC? BD?]

Answers