Conics

The curves known as conics were named after their historical discovery as the intersection of a plane with a right circular cone.
      
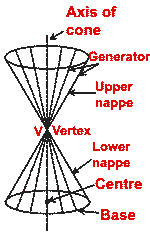
Applonius (before 200 B.C.) realized that a conic (or conic section) is a curve of intersection of a plane with a right circular cone of two nappes, and the three curves so obtained are parabola, hyperbola and ellipse.
    
Let l be a fixed line and F be a fixed point not on l, and e > 0 be a fixed real number. Let |MP| be the perpendicular distance from a point P (in the plane of the line l and point F) to the line l, then the locus of all points P such that |FP| = e |MP| is called a conic.
     
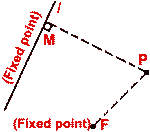
The fixed point F is called a focus of the conic and the fixed line l is called the directrix associated with F. The fixed real number e (> 0) is called eccentricity of the conic.
In particular, a conic with eccentricity e is called
(i) a parabola iff e = 1 (ii) an ellipse iff e < 1 (iii) a hyperbola iff e > 1.

Four standard forms of the parabola

     

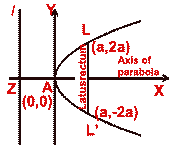
Main facts about the parabola

Equations y²= 4ax (a>0)
Right hand		 y² = -4ax
a>0
Left hand		 x² = 4ay
a>0
Upwards		 x² = -4ay
a>0
Downwards
Axis y=0 y = 0 x = 0 x = 0
Directrix x +a = 0 x -a = 0 y +a = 0 y -a = 0
Focus (a, 0) (-a, 0) (0,a) (0, -a)
Vertex (0,0) (0,0) (0,0) (0,0)
Length of Latus-rectum 4a 4a 4a 4a
Equation of Latus-rectum x -a = 0 x +a = 0 y -a = 0 y +a = 0
Focal distance of the point(x,y) x +a a -x y +a a -y

Another definition of ellipse

An ellipse is the locus of a point in a plane, sum of whose distances from two given points F and F' (in the plane) is a constant and greater than |FF'|.

Remark. The focal property of ellipse gives us a practical method of drawing an ellipse. Fasten the ends of a string of length 2a > |FF'| at two distinct points F and F'. Keep the string taught by means of a pencil placed against the string and slide it along the string, the curve thus traced is an ellipse with F and F' as its foci.

     

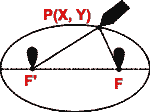
Main facts about the ellipse

Equation x²/a² + y²/b² = 1
a > b > 0		 x²/b² + y²/a² = 1
a > b> 0
Equation of major axis y = 0 x = 0
Length of major axis 2a 2a
Equation of minor axis x = 0 y = 0
length of minor axis 2b 2b
Vertices (a,0),(-a,0) (0, a),(0, -a)
Foci (ae, 0), (-ae,0) (0, ae), (0, -ae)
Directrices x - a/e = 0, x + a/e = 0 y - a/e = 0, y + a/e = 0
Length of Latus -rectuum 2b²/a 2a²/b
Equation of a latera-recta Center x-ae = 0, x +ae = 0
(0,0)		 y -ae = 0,y +ae = 0
Focal distance of any point (x,y) a -ex, a +ex a -ey, a +ey

   

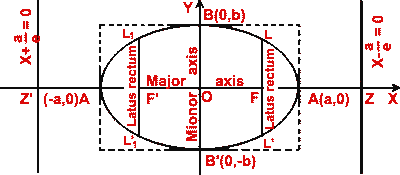
Another definition of hyperbola

A hyperbola is the locus of a point in a plane, the difference of whose distances from two given points F and F' is 2a (constant), and 0 < a < (1/2)|FF'.

     

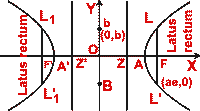
Main facts about the hyperbola

Equation x²/a² - y²/b²= 1
a > 0,b > 0		 y²/a² - x²/b² = 1
a > 0,b > 0
Length of transverse axis y = 0 x = 0
Equation of transverse axis 2a 2a
Length of conjugate axis 2b 2b
Equation of conjugate axis x = 0 y = 0
Vertices (a, 0), (-a, 0) (0, a), (0, -a)
Foci (ae, 0), (-ae, 0) (0, ae), (0, -ae)
Directrices x - a/e = 0, x + a/e=0 y - a/e= 0, y + a/e =0
Length of lactus-rectum 2b²/a 2a²/b
Equation of latera-recta
center		 x -ae = 0, x + ae = 0
(0,0)		 y -ae = 0,y + ae = 0
(0,0)
Focal Distance point(x,y) |ex -a|, |ex +a| |ey -a|,|ey +a|

Illustrative Examples

Example

Find the equation of the parabola with focus at (-2, 0) and whose directrix is the line x +2y -3 = 0.

Solution

The focus of the parabola is at F(-2, 0) and directrix is the line x +2y -3 = 0.
Let P(x, y) be any point on the parabola and |MP| be the perpendicular distance from P to the directrix, then by def. of parabola
   |FP| = |MP|         (As e = 1 for parabola)
So ((x +2)² +y²) = |x +2y -3|/(1² +2²)
On squaring,
=> 5 ((x +2)² +y²) = (x +2 y -3)²          (since |x|² = x²)
=> 5 (x² +4 +4 x +y²) = x² +4 y² +9 +4 x y -6 x -12 y
=> 4 x² -4 xy +y² +26 x +12 y +11 = 0,
which is the required equation of the parabola.

Example

Find the equation of the ellipse whose focus is (1, -2), the corresponding directrix x -y +1 = 0 and eccentricity is 2/3.

Solution

The focus of the ellipse is at F(1, -2), the corresponding directrix is the line x -y +1 = 0 and e = 2/3.
Let P (x, y) be any point on the ellipse and | MP | be the perpendicular distance from P to the directrix, then by def. of ellipse
 |FP| = e |MP|
=>
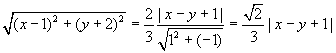
=> 9 [(x -1)² +(y +2)²] = 2 (x -y +1)²
=> 9 [x² -2 x +1 +y +1 +y² +4 y +4] = 2 [x² +y² +1 -2 x y +2 x -2 y]
=> 7 x² +4 x y +7 y² -22 x +40 y +43 = 0,
which is the required equation of the ellipse.

Example

Find the focus, directrix and eccentricity of the conic represented by the equation 3y² = 8x.

Solution

The given equation is 3 y² = 8 x     i.e. y² = (8/3) x ...(i)
which is the same as y² = 4ax, so (i) represents a standard (right hand) parabola, and hence its eccentricity is 1, as e = 1 for parabola.
Also 4a = 8/3 => a = 2/3, therefore, focus is (a, 0) i.e.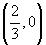 and the equation of directrix is
x +2/3 = 0 i.e. 3 x +2 = 0.

Example

Find the locus of a point P, the sum of whose distances from the points F(-2, 3) and F'(2, 0) is constant equal to 4 units.

Solution

Here, we note that |FF'| = [(2+2)² +(y -2)²] = 5
and |PF| +|PF'| = 4 (given)
=> |PF| +|PF'| < |FF'|, which is not possible wherever P may be (since sum of two sides of a triangle cannot be less than third side)
Therefore, the locus of P is the empty set.

Exercise

  1. Write the equation of a conic with eccentricity e, focus (a, 0) and directrix y-axis.
  2. Write the equation of a conic with eccentricity e, focus (0, a) and directrix x-axis.
  3. Write the equation of the parabola with the line x +y = 0 as directrix and the point (1, 0) as focus.
  4. Find the equation of the parabola whose focus is (2, -1) and directrix is x +2 y -1 = 0.
  5. Find the equation of the ellipse whose focus is (1, -1), the corresponding directrix is x -y +3 = 0 and e = 1/2.
  6. Find the equation of the hyperbola with directrix x +2 y = 1, focus at (0, 0) and eccentricity 2.
  7. Find the equation to the parabola with the focus (a, b) and directrix x/a + y/b = 1.
  8. Find the equation to the parabola whose focus is (-2, 1) and directrix is 6 x -3 y = 8.
  9. Find the equation of the parabola whose focus is (5, 3) and the directrix is given by 3x -4 y +1 = 0.also find the equation of axis.
  10. Find the equation to the conic section whose focus is (1, -1), eccentricity is 1/2 and the directrix is the line x -y = 3. Is the conic section an ellipse?
  11. Find the eccentricity of the ellipse if:
    (i) the latus-rectum is one half of its minor axis.
    (ii) the latus rectum is one half of its major axis.
    (iii) the distance between foci is equal to the length of latus-rectum.
  12. Find the eccentricity, co-ordinates of the foci and the length of the latus-rectum of the ellipse 4 x² +3 y² = 36.
  13. Find the co-ordinates of the foci and the ends of the latera-recta of the ellipse 16x² +9y² = 144.
  14. Find the vertices, eccentricity, foci and the equations of the directrices of the hyperbola x² -y² = 1.
  15. Find the lengths of axes, co-ordinates of foci, the eccentricity and the length of latus-rectum of the hyperbola 25 x² -9 y² = 225.
  16. In each of the parabolas
    (i) y² = 3 x    (ii) y² = -4 x    (iii) 3 x² = 4 y     (iv) x² = -12 y,
    find the length of latus-rectum, coordinates of focus and the equation of directrix.
  17. If the parabola y² = 4 p x passes through the point (3, -2), find the length of latus-rectum and the co-ordinates of the focus.
  18. Find the equation of the parabolas with vertices at the origin and satisfying the following conditions:
    (i) Focus at (-4, 0)       (ii) Directrix y -2 = 0
    (iii) Passing through (2, 3) and axis along x-axis.
  19. Find the equation to the ellipse referred to its axes as co-ordinates axes
    (i) whose major axis = 8, eccentricity = 1/2
    (ii) which passes through the points (-3, 1) and (2, -2).
    (iii) which passes through the point (-3, 1) and has eccentricity .
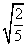    (iv) whose minor axis is equal to the distance between foci and whose latus-rectum is 10.
  20. Find the equation of the ellipse whose eccentricity is 1/2 and whose foci are (±2, 0).

Answers

1. (1 -e²) x² +y² -2 a x +a² = 0
2. x² +(1 -e²) y² -2 ay +a² = 0
3.(x -y)² -4 x +2 = 0
4. 4 x² -4x y +y² -18 x +14 y +24 = 0
5. 7 x² +2 x y +7 y² -22 x +22y +7 = 0
6. x² +82x y +5 y² -8 x -8y +4 = 0
7. a² x² -2 a b x y +b² y² -2 a³ x -2 b³ y +(a 4 - a² b² +b4) = 0
8. 9 x² +36 x y +36 y² +276 x -138 y -169 = 0
9.16 x² +24 x y +9 y² -256 x -142 y +849 = 0; 4x +3 y -29 = 0
10. 7 x² +2 x y +7 y² -10 x +10 y +7 = 0; Yes
11. (i) (3)/2    (ii) 1/2      (iii) (5 1)/2
12. e = 1/2, foci are (0,3), (0, -3), length of latus-rectum = 33
13. (0, 7), (0, -7);
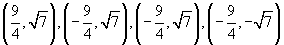
14. (1, 0), (-1, 0); 2  ; (2, 0), (-2 , 0); 2 x -1 = 0, 2x +1 = 0
15. 6, 10; (34 , 0), (-34, 0); (34)/3; 10
16. (i) 2 3 ((3)/2, 0) ; 2 x + 3 = 0 (ii) 4; (-1, 0); x -1 = 0
     (iii) 4/3 ; (0, 1/3) ; 3 y +1 = 0        (iv) 12; (0, -3); y -3 = 0
17. 4/3, (1/3, 0)
18. (i) y² = -16 x    (ii) x² = -8y   (iii) 2 y² = 9 x
19. (i) 3 x² +4 y² = 48  (ii) 3x² +5 y² = 32
     (iii) 3 x² +5 y² = 32  (iv) x² +2y² = 100
20. 3 x² +4 y² = 48