(i) (cos
(ii) cos n
The theorem is stated in two steps as follows:
(i) (cos ![]() +i sin
+i sin ![]() )n = cos n
)n = cos n ![]() +i sin n
+i sin n ![]() , if n is an integer (positive, zero or negative)
, if n is an integer (positive, zero or negative)
(ii) cos n ![]() +i sin n
+i sin n ![]() is one of the
values of (cos
is one of the
values of (cos ![]() + i sin
+ i sin ![]() )n
if n is a non integral rational number.
)n
if n is a non integral rational number.
Let z = r cos ![]() = r cos (
= r cos (![]() +2 m
+2 m
![]() ), where m
), where m ![]() I
I
z1/n = r1/n ![]()
Note that r1/n is a real, positive number. Putting m = 0, 1, 2, ...
n -1 we get n distinct roots of z, and then the values of
![]() start repeating.
start repeating.
Since 1 = 1 +0 i = cis 0 = cis (0 +2m![]() ) = cis 2m
) = cis 2m![]() ,
m
,
m ![]() I,
I,
11/3 = (cis 2m![]() )1/3 = cis 2m
)1/3 = cis 2m![]() /3
where m = 0, 1, 2
/3
where m = 0, 1, 2
= cis 0, cis 2![]() /3, cis 4
/3, cis 4![]() /3
/3

= 1, (-1 +![]() 3 i)/2, (-1 -
3 i)/2, (-1 -![]() 3 i)/2
3 i)/2
Putting w = (-1 +![]() 3 1)/2
3 1)/2

= (1 -3 -2![]() 3 i)/4 = (-1 -
3 i)/4 = (-1 -![]() 3 i)/2
3 i)/2
Hence three cube roots of unity are 1, w, w² where w = (-1 +![]() 3 i)/2
3 i)/2
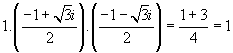 ,
thus w³ = 1.
,
thus w³ = 1.If z = (13 -5 i)/(4 -9 i), find z6.
Given z = (13 -5 i)/(4 -9 i) =[(13 -5 i)(4 +9 i)]/[(4 -9i)(4 +9i)]
= (97 +97 i)/97
= 1 + i/4 = ![]() 2 [cos(
2 [cos(![]() /4) + i sin (
/4) + i sin (![]() /4)]
/4)]
Using Demoivre theorem,
z6 = 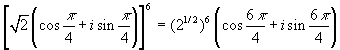
= 8(cos 3![]() /2 +i sin 3
/2 +i sin 3![]() /2) = 8[0 +i(-1)]
= -8i
/2) = 8[0 +i(-1)]
= -8i
Convert the following number to standard form x +iy
(cos ![]() +i sin
+i sin ![]() )7
(cos
)7
(cos ![]() -i sin
-i sin ![]() )³
)³
(cos ![]() +i sin
+i sin ![]() )7 (cos
)7 (cos ![]() -i sin
-i sin ![]() )³ = (cis
)³ = (cis ![]() )7
(cis (-
)7
(cis (- ![]() ))³
))³
= (cis ![]() )7 ((cis
)7 ((cis
![]() )-1)³ = (cis
)-1)³ = (cis ![]() )7
(cis
)7
(cis ![]() )-3
)-3
= (cis ![]() )4 =
cis 4
)4 =
cis 4 ![]() = cos 4
= cos 4 ![]() +i sin 4
+i sin 4 ![]() .
.
Given that one of the roots of x4 -2 x³ +3 x² -2 x +2 = 0 is 1 +i, find the other three roots.
Since all the coefficients of the given equation are real numbers, the
roots, if complex, occur in conjugate pairs. Thus two roots are 1 +i, 1 -i.
Hence x -(1 +i), x -(1 -i) are two factors of given equation,
i.e. (x -(1 +i))(x -(1 -i)) = x² -2 x +2 is a factor of given equation.
Now it is easy to see that x4 -2 x³ +3 x² -2 x +2 = (x² -2x +2)(x²
+1).
Also we know that x² +1 = (x -i)(x +i).
Thus the four roots of the given equation are ±i, 1 ±i.
Find the fourth roots of unity.
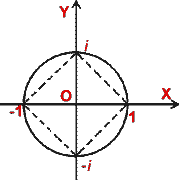
1 = 1 +0 i = cis 0
= cis (0 +2 m![]() ) = cis 2m
) = cis 2m![]() ,
where m
,
where m ![]() I,
I,
11/4 = (cis 2 m ![]() )1/4 = cis 2m
)1/4 = cis 2m![]() /4,
where m = 0, 1, 2, 3
/4,
where m = 0, 1, 2, 3
= cis 0, cis ![]() /2, cis
/2, cis ![]() , cis 3
, cis 3![]() /2
/2
= 1, i, -1, -i.
Hence the fourth roots of unity are ±1, ±i.
Show that
(i) (1 +w -w²)6 = 64.
(ii) (1 -w +w²)7 +(1 +w -w²)7 = 128.
(iii) (2 -w)(2 -w²)(2 -w10)(2 -w11) = 49.
(i) (1 +w -w²)6 = (-w² -w²)6
[using 1 +w +w² = 0]
= (-2w²)6 = 26
w12 = 64(w³)4 = 64 [using w³ = 1]
(ii) (1 -w +w²)7 +(1 +w -w²)7 = (-w -w)7 +(-w² -w²)7
= -27. w7 -27 w14 = -27[(w³)².
w +(w³)4. w²]
= -27. (w +w²) = -27. (-1) = 128.
(iii) (2 -w)(2 -w²)(2 -w10)(2 -w11)
= [4 -2(w +w²) +w³] [4 -2w10(1 +w) +w21]
= [4 -2(-1) +1] [4 -2w (-w²) +1]
(why?)
= (4 +2 +1)(4 +2. 1 +1) = 7. 7 = 49.
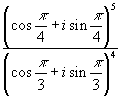
 (v) cube roots of 64.
(v) cube roots of 64.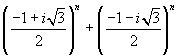 is equal to
is equal to