Geometric Mean
When three numbers are in G.P., the middle one is said to be the geometric
mean (briefly written as G.M.) between the other two.
Let a, b be two (positive) numbers and G be the G.M. between them. Then, by
definition, a, G, b are in G.P.
=> G = b => G² = a b => G =  ab
ab
(Conventionally, G is taken as positive).
Thus the G.M. between two numbers a and b is G =  ab
ab
Similarly, if a, G1, G2, ..., Gn, b are in
G.P., then G1, G2, ..., Gn are called n
geometric means between a and b.
Illustrative Example
Example
- The A.M. between two numbers is 34 and G.M. is 16. Find the numbers.
- Show that A.M. between two distinct positive numbers is always greater
than G.M.
- If x, y, z are distinct positive numbers, prove that
(x +y)(y +z)(z +x) > 8 x y z.
Further if x +y +z = 1, show that (1 -x)(1 -y)(1 -z) > 8 x y z.
Solution
- Let the two numbers be a and b. Then A.M. = (a +b)/2 = 34
=> a +b = 68
G.M. =  ab = 16
ab = 16
=> a b = 256 => a (68 -a) = 256
=> a² -68 a +256 = 0 => (a -64)(a -4) = 0
=> a = 4, 64
Taking a = 64, we get b = 68 -a = 4
Taking a = 4, we get b = 68 -a = 64
Thus the two numbers are 4 and 64
- Let a, b be two given positive real numbers. Then A.M. = A = (a + b)/2
G.M. = G =  ab
ab
Therefore, A -G = (a +b)/2 -  ab = (1/2)(a +b -2
ab = (1/2)(a +b -2 ab)
= (1/2)(
ab)
= (1/2)( a -
a -  b)²
b)²
Now ( a -
a -  b)²,
being the square of a non-zero real number is positive.
b)²,
being the square of a non-zero real number is positive.
A -G > 0 => A> G
- As the A.M. between two distinct positive numbers is greater than the G.M. between them, therefore
(x + y)/2 >  xy => x
+y > 2
xy => x
+y > 2 xy ....(1)
xy ....(1)
(y + z)/2 >  yz =>
z + y > 2
yz =>
z + y > 2 yz ...(2)
yz ...(2)
(z + x)/2 >  zx =>
x + z > 2
zx =>
x + z > 2 zx ...(3)
zx ...(3)
From (1), (2) and (3), we get
(x +y)(y +z)(z +x) > 2 x
y 2
x
y 2 y z 2
y z 2 z x
z x
i.e. (x +y)(y +z)(z +x) > 8 x y z
...(4)
When x +y +z = 1, then
y +z = 1 -x, z +x = 1 -y and x +y = 1 -z
(1 -x)(1 -y)(1 -z)> 8 x y z.
[using (4)]
Exercise
- (i) Insert 3 geometric means between 1 and 256.
(ii) Insert 4 geometric means between 4/9 and 27/8.
(iii) Insert 5 geometric means between 576 and 9. Show that their product is
equal to the fifth power of the single G.M. between the given numbers.
- (i) The A.M. of two numbers a and b exceeds their G.M. by 2. The ratio of
two numbers is 4. Find the numbers.
(ii) Find two positive numbers whose difference is 12 and whose A.M. exceeds G.M. by 2.
- Find the value of n so that
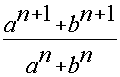 may be the G.M. between a and b.
may be the G.M. between a and b.
- If one geometric mean G and two arithmetic means p and q are inserted
between two numbers, show that G² = (2 p -q)(2 q -p).
- Show that if A and G are A.M. and G.M. between two positive numbers, then
the numbers are A ±
 (A² -G²).
(A² -G²).
- If the A.M. and G.M. between two numbers are in the ratio m : n, then
prove that the numbers are in the ratio m +
 (m² -n²) : m
-
(m² -n²) : m
- (m² -n²)
(m² -n²)
- If G is the geometric mean between a and b, show that
1/(G + a) + 1/(G+b) = 1/G
- If G1 and G2 are two geometric means between a and
b, show that
(i) G1 G2 = a b
(ii) G1² / G2 + G2²/G1 = a +b
- If p, q, r are in A.P., a is G.M. between p and q, and b is G.M. between q and r,
then prove that a², q², b² are in A.P.
Answers
1. (i) 4, 16, 64
(ii) 2/3, 1, 3/2, 9/4
(iii) 288, 144, 72, 36, 18
2. (i) 16, 4
(ii) 16, 4
3. -1/2
![]() ab
ab![]() ab
ab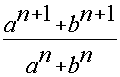 may be the G.M. between a and b.
may be the G.M. between a and b.