Geometric Progression (G.P.)
A sequence (finite or infinite) of non-zero numbers is called a
geometric progression (abbreviated G.P.) iff the ratio of any term
to its preceding term is constant. This non-zero constant is usually denoted
by r and is called common ratio.
General term of a G. P.
Tn = a rn-1
Thus, if a is the first term and r is the common ratio., then the G.P. is a,
ar, ar², ..., arn -1 or a ,ar, ar², ar³, ... according as it is
finite or infinite.
Remarks
- If the last term of a G.P. consisting of n terms is denoted by l,
then l = a. rn-1.
- Three numbers a, b, c are in G.P. iff b/a = c/b i.e. iff b² = ac.
- Sometimes the problem involves 3, 4 or 5 numbers in a G.P. If the product
of the numbers is given, then in a G.P.,
(i) three numbers are taken as a/r, a, ar.
(ii) four numbers are taken as a/r³, a/r, a r, ar³.
(iii) five numbers are taken as a/r², a/r, a, a r, ar².
Illustrative Examples
Example
Find the n th and the 15th term of the series
1 - 1/2 + 1/4 - 1/8 ....
Solution
The given series is a G.P. with first term a = 1 and common ratio r = -1/2.
Hence nth term,

In particular, T15 = (-1)15-1. 21-15 = 2-14.
Example
Three numbers whose sum is 21 are in A.P. If 2, 2, 14 are added to them
respectively, the resulting numbers are in G.P. Find the numbers.
Solution
Let the three given numbers in A.P. be a -d, a, a +d.
Their sum = 3a = 21 => a = 7.
Hence the numbers are 7 -d, 7, 7 +d.
Adding 2, 2, 14 respectively, we get the numbers 9 -d, 9, 21 +d.
Since these three are in G.P.,
(9)² = (9 -d)(21 +d) => d² +12d -108 = 0
=> (d +18)(d -6) = 0 => d = 6 or -18.
Using d = 6, we get three numbers as 1, 7, 13, and using d = -18, we get three
numbers as 25, 7, -11. Thus two sets of numbers are 1, 7, 13 or 25, 7, -11.
Example
- If a, b, c, d are in G.P., prove that a +b, b +c, c +d are also in G.P.
- Find all sequences which are simultaneously arithmetic and geometric progressions.
Solution
- Given a, b, c, d are in G.P., let r be the common ratio.
So b = ar, c = ar², d = ar³.
Hence (b +c)² = (ar +ar²)² = a²r²(1 +r)²,
and (a +b)(c +d) = (a +ar)(ar² +ar²) = a²r²(1 +r)².
Hence (b +c)² = (a +b)(c +d) => a +b, b +c, c +d are in G.P.
- Let a1, a2, ..., an, ... be a sequence
which is A.P. as well as G.P. Since it is an A.P.,
an +1 =
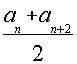 , n
, n  1
1
Also, since it is a G.P., Let a1 0 and r be the
common ratio,
0 and r be the
common ratio,
so an = a1. rn -1, an +1 = a1.
rn, an+2 = a1. rn +1.
Substituting these values in above equation, we get
a1 rn =

=> r = (1 +r²)/2 => r² -2 r +1 = 0
=> (r -1)² = 0 => r = 1
Therefore, only a constant sequence a, a, a, ... (a 0) is
both an A.P. and G.P.
0) is
both an A.P. and G.P.
Example
If a, b, c are the p th, q th and r th terms respectively of an A.P. and
also the pth, qth and rth terms of a G.P., prove that ab -c. bc
-a. ca -b = 1.
Solution
Let the A.P. be A, A +D, A +2 D, ... and G.P. be x, xR, xR², ... then
a = A +(p -1)D, b = A +(q -1)D, c = A +(r -1)D
=> a -b = (p -q)D, b -c = (q -r)D, c -a = (r -p)D
Also a = xRp -1, b = xRq-1, c = xRr -1
Hence ab -c.bc -a.ca-b = (xRp -1)(q
-r)D.(xRq -1)(r -p)D. (x Rr -1)(p -q)D
= x(q -r +r -p +p -q)D.
R[(p -1)(q -r) +(q -1)(r -p) +(r -1)(p -q)]D
= x°. R° = 1.1 = 1
Exercise
- (i) Find the next term of the sequence 1/6, 1/3, 2/3...
(ii) Find the 15th term of the series  3 +1/
3 +1/ 3
+1/3
3
+1/3 3 +...
3 +...
- Which term of the series
(i) 1 +1/3 +1/9 +1/(27)....is 1/(243)
(ii) 3 -3 3 +9 -... is 729?
3 +9 -... is 729?
- (i) Determine the 12th term of a G.P. whose 8th term is 192 and common ratio is 2.
(ii) Find the number of terms of a G.P. whose first term is 3/4, common ratio
is 2 and the last term is 384.
(iii) Find the geometric series whose 4th term is 54 and the 7th term is 1458.
(iv) The fourth term of a G.P. is the square of its second term and the first
term is -3. Determine its seventh term.
- Find the value of x such that
(i) -2/7, x, -7/2 are three consecutive terms of a G.P.
(ii) x +9, x -6 and 4 are three consecutive terms of a G.P.
(iii) x, x +3, x +9 are first three terms of a G.P.
- (i) Three numbers are in A.P. and their sum is 15. If 1, 4 and 19 are
added to these numbers respectively, the resulting numbers are in G.P. Find the numbers.
(ii) Three numbers whose sum is 70 are in G.P. If each of the extremes is
multiplied by 4 and the mean by 5, the numbers will be in A.P. Find the numbers.
- (i) The lengths of the sides of a triangle form a G.P. If the perimeter
of the triangle is 37 cm and the shortest side is of length 9 cm, find the
lengths of the other two sides.
(ii) There are four numbers such that first three of them form an arithmetic
sequence and the last three form a geometric sequence. The sum of the first
and third terms is 2 and that of second and fourth is 26. What are these numbers?
(iii) The sum of first three terms of a G.P. is 7 and the sum of their
squares is 21. Determine the first five terms of the G.P.
[Hint. Let the three terms be a, ar and ar².Use r4 +r² +1 =
(r² +r +1)(r² -r +1)]
- (i) If a, b, c are in A.P. as well in G.P., prove that a = b = c.
(ii) Consider a G.P. of finitely many terms. Prove that product of n th term
from the beginning and nth term from the end is a constant and equals to the
product of first and the last terms.
(iii) The terms of a G.P. with first term a and common ratio r are squared.
Prove that resulting series is also a G.P. Find its first term, common ratio
and the n th term.
- (i) If a, b, c are in G.P. show that 1/a, 1/b, 1/c are also in G.P.
(ii) If K is any positive real number and Ka, Kb, Kc
are three consecutive terms of a G.P., prove that a, b, c are three
consecutive terms of an A.P.
(iii) If p, q, r are in A.P., show that p th, q th and r th terms of any G.P.
are themselves in G.P.
- If a, b, c, d are in G.P., show that
(i) a² +b², b² +c², c² +d² are in G.P.
(ii) a² -b², b² -c², c² -d² are in G.P.
(iii) (a² +b² +c²)(b² +c² +d²) = (ab +bc +cd)²
(iv) (b -c)² +(c -a)² +(d -b)² = (a -d)².
- Does there exist a geometric progression containing 27, 8 and 12 as three
of its terms? If it exists, how many such progressions are possible?
[Hint. Take 27, 8, 12, as p th, q th, r th items. We get p +2 q = 3 r,
which has infinite number of positive integral solutions.]
Answers
1. (i) 4/3 (ii) 3-27/2
2. (i) 6th (ii) 11th
3. (i) 3072 (ii) 10
(iii) 2 +6 +18 +54 +... (iv) -2187
4. (i) ±1 (ii) 0 or 16 (iii) 3
5. (i) 2, 5, 8 or 26, 5, -16 (ii) 10, 20, 40
6. (i) 12 cm, 16 cm
(ii) -3, 1, 5, 25 or 7, 1, -5, 25
(iii) 1, 2, 4, 8, 16 or 4, 2, 1/2 , 1/4, 1
7. (iii) a², r², a² r2n -2
10. Yes, infinite many
![]()
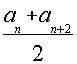 , n
, n