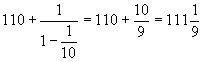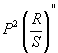Sum of first n Terms of a G.P.
Formulae
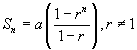
This formula can also be written as
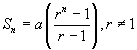
Note that if r = 1, this formula can not be used. In that case
Sn = a +a +a +... n times = na.
Sum of an infinite G.P.
When r < 1 numerically i.e. -1 < r < 1, then rn goes on decreasing numerically as n increases, and ultimately
as n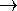
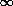 , rn
, rn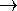 0
0
 as n
as n 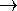
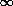
The limiting sum of the G.P. a +a r +a r² +... to 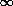 is a/(1 - r) when |r| < 1.
is a/(1 - r) when |r| < 1.
Note that if |r| 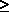 1, the G.P. diverges, and sum can not be found.
1, the G.P. diverges, and sum can not be found.
Zeno's Paradox
Ancient mathematicians did not know the idea of limits, and they devised
several paradoxes of endlessness. In Zeno (5th century B.C) paradox, Achilles and
the tortoise had a race. Achilles could run 10 times as fast as the tortoise, but the
tortoise had a hundred yard start. Achilles runs the hundred yards, but the tortoise is now
10 yards ahead. Achilles runs the 10 yards, but the tortoise is now 1 yard ahead.
Achilles runs the 1 yard, but the tortoise is now
1/10 yard ahead, and so on. How can Achilles overtake the tortoise? The ancient Greeks
did not know about limits, so in their logic the problem could not be solved. However, we know
that 100 +10 +1 +1/10 + 1/100 ... has a limiting sum
= 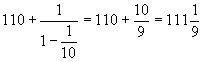
and so at this point, Achilles overtakes the tortoise.
Exercise
- Find the sum of
(i) 20 terms of the series 2 +6 +18 +...
(ii) 10 terms of series 1 + 3 +3 +...
3 +3 +...
(iii) 6 terms of 1, -2/3 , 4/9,...
(iv) 100 terms of 0·7 +0· 07 +0· 007 +...
(v) the series 81 -27 +9 ... -1/27
- Sum the following series to infinity:
7 -1 + 1/7 - 1/49 + ....
- (i) How many terms of the sequence 1, 4, 16, ... must be taken to have their sum equal to 341?
(ii) How many terms of the sequence 3, 3/2, 3/4 ... are needed to give the sum 3069/512?
(iii) How many terms of the sequence 1,  2, 2,
2
2, 2,
2 2, ... are required to give a sum of
1023(
2, ... are required to give a sum of
1023( 2 +1)?
2 +1)?
- (i) If the first term of a G.P. is 5 and the sum of first three terms is
31/5, find the common ratio.
(ii) The sum of first three terms of a G.P. is to the sum of first six terms as 125 : 152.
Find the common ratio of the G.P.
(iii) In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common
ratio.
(iv) The sum of first three terms of a G.P. is 16 and sum of the next 3 terms is 128.
Determine the first term, common ratio and sum to n terms of the G.P.
- The first term of an infinite G.P. is 1 and any term is equal to the sum of all the succeeding
terms. Find the series.
- Find the sum of first n terms of the series
(i) 3 +33 +333 +...
(ii) 0· 4 +0· 44 +0· 444
- A snail starts moving towards a point 3 cms away at a pace of 1 cm per hour. As he gets
tired, he covers only half the distance compared to previous hour in each succeeding hour.
In how much time will the snail reach his target?
- If S be the sum, P the product and R the sum of reciprocals of n terms of a geometric
progression, find the value of
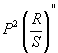
- The sum of an infinite G.P. is 16 and the sums of the squares of its terms is
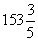 .
Find the common ratio and fourth term of the progression.
.
Find the common ratio and fourth term of the progression.
- Find the sum of an infinite G.P. whose first term is 28 and the fourth term is 4/49.
- Find the sum of divisors of 762048.
[Hint. Given number = 26. 35. 7²; sum of divisors is
(1 +2 +2² +... +26)(1 +3 +3² +... +35)(1 +7 +7²) as the
expansion contains all possible divisors]
Answers
1. (i) 320 -1 (ii) 121( 3 +1)
(iii) 133/243
3 +1)
(iii) 133/243
(iv) 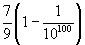 (v)
(v)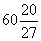
2. 49/8
3. (i) 5
(ii) 10 (iii) 20
4. (i) 1/5 or -6/5 (ii) 3/5 (iii) 2
(iv) 16/7, 2, 16(2n -1)/7
5. 1, 1/2, 1/4, 1/8
6. (i) (1/27)(10n+1 -9 n -10)
(ii) 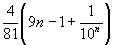
7. Never
8. 1
9. 1/4, 3/16
10. 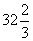 11. 2634996
11. 2634996
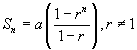
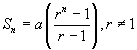
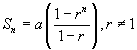
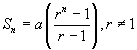
![]()
![]() , rn
, rn![]() 0
0 as n
as n ![]()
![]()
![]() is a/(1 - r) when |r| < 1.
is a/(1 - r) when |r| < 1.![]() 1, the G.P. diverges, and sum can not be found.
1, the G.P. diverges, and sum can not be found.