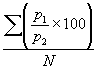
Index number is a specialized average designed to measure the change in the level of an activity or item, either with respect to time or geographic location or some other characteristic. It is described either as a ratio or a percentage. For example, when we say that consumer price index for 1998 is 175 compared to 1991, it means that consumer prices have risen by 75% over these seven years.
Wholesale Price Index(WPI) and Consumer Price Index (CPI) are widely used terms. They indicate the inflation rates, and also changes in standard of living. Consumer price index is based on prices of five sets of items - Food, Housing (Rent), Household goods, Fuel and light, and Miscellaneous. Each item is based on study of a number of items - e.g. Food includes Rice, Wheat, Dal, Milk, and so on.
Price Relative means the ratio of price of a certain item in current
year to the price of that item in base year, expressed as a percentage (i.e.
Price Relative = (p2/p1)×100). For example, if a
colour TV cost Rs 12000 in 1981 and Rs. 18000 in 1998, the price relative is
(18000/12000)×100 = 150.
Generally instead of one item, rates of a number of items are given, for current year as well as for base year. Sometimes different weights, or quantities are also given for those items. There are a number of ways to calculate index numbers in such cases.
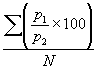


During a certain period, the cost of living index number goes from 110 to 200 and the salary of a worker is also raised from Rs 325 to Rs. 500. Does the worker really gains or loses, and by how much amount in real terms?
Real wage = [(Actual wage)/(cost of living index)] × 100
So real wage of Rs 325 = (325/110) × 100 = Rs 295·45
and real wage of Rs 500 = (500/200) × 100 = Rs 250
So the worker actually loses, i.e. Rs (295·45 -250)
= Rs 45·45 in real terms.
With price index of 1991 as 100, the cost of living index for 1996 is 160 and for 1997 is 180. The salary of an employee increased from Rs 5000 in 1996 to Rs 5500 in 1997. Find out whether the real income in 1997 has increased or decreased as compared to 1996. Also calculate if any extra dearness allowance should be paid to him to compensate for loss. Also calculate purchasing power of rupee in 1996 and 1997.
The price relative of 1997 compared to 1996 is
I = (p2/p1)×100 = (180/160)×100 = 112·50.
Hence the wages of Rs 5500 in 1997 are equal to wages of
(5500×100)/112.50 = Rs 4889 in 1996.
Thus we find that real income in 1997 has decreased compared to 1996.
Now let us assume that Rs x extra dearness allowance is paid to compensate for
this loss.
Hence (5500+x)/180 = 5000/160 => x = Rs 125
Now purchasing power of a rupee is defined as
Purchasing power = (Index number for base year)/(Index number for current year)
So purchasing power of rupee in 1996 compared to 1991 is
Rs 100/160 = paise (100/160) × 100 = 62·5 paise
![]() 62 paise
62 paise
Purchasing power of rupee in 1997 compared to 1991 is
Rs = 100/180 paise = (100 × 100)/180 = 55·55 paise
![]() 56 paise
56 paise
Thus we see that due to inflation (price rise), the purchasing power of rupee is falling.
Using 1985 as base year, the index numbers for the price of a commodity in 1986 and 1987 are 118 and 125. Calculate the index numbers for 1985 and 1987 if 1986 is taken as the base year.
Let p1, p2, p3 be prices in 1985, 1986,
1987.
Then p1/p2 × 100 = 118 and p3/p2 ;× 100 = 125
Now price index of 1985 with 1986 as base
= p1/p2 × 100 = (100/118) × 100 = 84·75
Price index of 1987 with 1986 as base
= 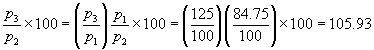
This procedure is called shifting of base.
| Commodity | Base Price | Current Price |
| Rice | 140 | 180 |
| Oil | 400 | 550 |
| Sugar | 100 | 250 |
| wheat | 125 | 150 |
| Fish | 200 | 300 |
| Weight | Price index | |
| Food | 35 | 108.5 |
| Rent | 9 | 102.6 |
| Clothes | 10 | 97.0 |
| Fuel | 7 | 100.9 |
| Miscellaneous | 39 | 103.7 |
| Butter | Bread | Tea | Bacon | |
| Relative Index | 181 | 116 | 110 | 152 |
| Weight | 4 | 12 | 3 | 7 |
| Commodity | A | B | C | D | E |
| 1988 Price per unit(Rs) | 16.00 | 40.00 | 0.50 | 5.12 | 2.00 |
| 1988 Price per unit(Rs) | 20.00 | 60.00 | 0.50 | 6.25 | 1.50 |
| Commodity | A | B | C | D |
| Price per unit in 1995 | 20 | 10 | 25 | 40 |
| Price per unit in 1999 | 24 | 20 | 30 | 40 |
| Commodity | A | B | C | D |
| Price per unit in 1995 | 10 | 20 | 5 | 40 |
| Price per unit in 1995 | 30 | 35 | 10 | 80 |
| Weight | 20 | 30 | 10 | 40 |
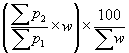 = 212·5
10. 250
= 212·5
10. 250