Line and Circle

The condition that the line y = mx +c may intersect the circle x² + y² = a² is given by
               a²(1 + m²) 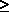c²

Remark

The line y = m x + c will intersect the circle x² + y² = a² in two distinct points iff a² (1 +m²) > c², and the line will intersect the circle in one and only one point i.e. the line will be a tangent to the circle iff a²(1 +m²) = c², and the line will not intersect the circle iff a²(1 + m²) < c².

Corollary 1. Condition of the tangency

The line y = mx + c will touch the circle x² +y² = a²
   iff a²(1 + m²) = c² i.e. iff c = ± a [1 +m²]

Corollary 2. Equations of tangents in slope form

Substituting the values of c = ± a [1 +m²] in equation y = mx + c, we get
    y = mx ± a[1 +m²]
Thus, there are two parallel tangents to the circle x² +y² = a² having m as their slope.

Length of intercept made by a circle on a line

Let a line l meet a circle S with center C and radius r in two distinct points. If d is the distance of C from l then the length of intercept = p [r² -d²]

Length of tangent

Let S be a circle and P be an exterior point to S, and PT1, PT2 be two tangents to S through P, then the distance |PT1| or |PT2| is called the length of tangent from P to the circle S.
The length of tangent =

                  

Illustrative Examples

Example

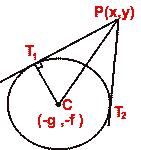
Find the locus of the point of intersection of perpendicular tangents to the circle x² +y² = a²

                     

Solution

he given circle is x² + y² = a²       ...(i)
The equation of any tangent to the circle (i) in the slope form is
       y = mx +a[1 +m²]                             .... (ii)
Let (ii) pass through the point P (, ), then
     = m + a[1 +m²]
      - m = a[1 +m²]
=> ( - m)² = a²(1 + m²)
=>  ² + m 2² - 2m - a² - a² m² = 0
=>  (² - a²) m² - 2m + (² - a²) = 0,
which is a quadratic in m having two roots, say m1, m2; and these represent slopes of two tangents passing through P (, ).
Since the tangents are at right angles, m1 m2 = -1
=>  ² - a² = -1 =>   ² - a² = -² + a² ² -a²
=>  ² + ² = 2 a²
The locus of P (, ) is x² +y² = 2 a²
Thus, the locus of point of intersection of perpendicular tangents to the circle x² +y² = a² is x² +y² = 2 a², which is a circle concentric with the given circle.
This is known as director circle of the circle x² +y² = a².

Exercise

  1. Determine the number of points of intersection of the circle x² +y² + 6x -4y +8 = 0 with each of the following lines:
    (i) 2 x + y -1 = 0
    (ii) x +1 = 0
    (iii) 4x +3y -12 = 0
  2. Determine the points of intersection (if any) of the circle x² +y² +5 x = 0 with each of the following lines:
    (i) x = 0
    (ii) 3x - y +1 = 0
    (iii) 3x -4 y = 7
  3. Find the points in which the line y = 2 x +1 cuts the circle x² + y² = 2. Also find the length of the chord intercepted.
  4. (i) Find the points of intersection of the circle 3 x² +3 y² -29 x -19 y -56 = 0 and the line y = x +2. Also find the length of the chord intercepted.
    (ii) If y = 2 x is a chord of the circle x² + y² -10 x = 0, find the equation of the circle with this chord as diameter. Hence find the length of the chord intercepted.
  5. Find the lengths of intercepts made by the circle x² + y² -4 x -6 y - 5 = 0 on the co-ordinate axes.
  6. Find the length of the chord intercepted by the circle x² +y² -8 x -6 y = 0 on the line x -7 y -8 = 0.
  7. Find the length of the chord intercepted by the circle x² +y² = 9 on the line x +2 y = 5. Determine also the equation of the circle described on this chord as diameter.
    [Hint. The center of the circle described on the chord x +2 y = 5 as diameter is the point of intersection of this line and the line through (0, 0) and perpendicular to this line.]
  8. (i) Prove that the lines x = 7 and y = 8 touch the circlex² + y² -4 x -6 y -12 = 0. Also find points of contact.
    (ii) Find the co-ordinates of the center and the radius of the circle x² + y² -4 x +2 y -4 = 0. Hence, or otherwise, prove that x +1 = 0 is a tangent to the circle. Calculate the co-ordinates of the point of contact. If this point of contact is A, find the co-ordinates of the other end of the diameter through A.
  9. Prove that the line y = x +a2 touches the circle x² +y² = a². Also find the point of contact.
  10. Prove that the line 4 x +y -5 = 0 is a tangent to the circle x² + y² +2 x -y -3 = 0, also find the point of contact.
  11. Find the condition that the line l x +m y + n = 0 may touch the circle x² +y² = a².
  12. Find the condition that the line l x + m y +n = 0 may touch the circle x² +y² +2 g x +2 f y + c = 0.
  13. If the circle 2 x² +2 y² = 5 x touches the line 3 touches the line 3 x + 4 y = k, find the values of k.
  14. (i) Find the equation of the circle with center (3, 4) and which touches the line 5x +12y -1 = 0.
    (ii) Find the equation of the circle whose center is (4, 5) and touches the x-axis. Find the co-ordinates of the points at which the circle cuts y-axis.
  15. Find the equation to the circle concentric with x² +y² -4 x -6 y -3 = 0 and which touches the y-axis.
  16. Find the equation to the circle which is concentric with x² +y² -6 x +7 = 0 and touches the line x +y +3 = 0.
  17. Find the length of the chord made by the x-axis with the circle whose center is (0, 3 a) and which touches the straight line 3 x +4 y = 37.
  18. Show that 3 x -4 y +11 = 0 is a tangent to the circle x² + y² -8y +15 = 0 and find the equation of the other tangent which is parallel to the line 3 x = 4 y.
  19. Find the equations of the tangents to the circle x² +y² = 25 which are parallel to the line y = 2 x +4.
  20. Find the equations of the tangents to the circle x² +y² -2 x -4 y = 4 which are perpendicular to the line 3 x - 4 y -1 = 0.

Answers

1. (i) one point      (ii) two distinct points       (iii) none
2. (i) (0, 0)          (ii) (-1, -2), (-1/10, 7/10) (iii) none
3.(-1, -1),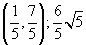
4. (i) (1, 3), (5, 7) ; 42      (ii) x² + y² -2 x -4 y = 0 ; 25
5. Intercept on x-axis = 6, intercept on y-axis = 214
6. 52                                 7. 4; x² +y² -2 x -4 y +1 = 0
8. (i) (7, 3), (2, 8)
   (ii) (2, -1), 3; point of contact (-1, -1), other end of diameter (5, -1)
9. (-a/2, a/2)                   10. (1, 1)
11. n = ± a[l² +m²]
12. (l g + m f -n)² = (l² + m²)(g² + f² -c)
13. 10, 5/2
14. (i) 169 (x² + y² -6 x -8 y) +381 = 0
     (ii) x² + y² -8 x -10 y +16 = 0; (0, 2), (0, 8)
15. x² + y² -4 x -6 y +9 = 0
16. x² + y² -6 x -9 = 0
17. 8 | a |                             18. 3 x -4 y +21= 0
19. 2 x - y ± 55 = 0
20. 4 x + 3 y +5 = 0, 4 x +3 y -25 = 0