Families of Lines

One parameter family of lines

It may seem that the equation of a straight line ax +by +c = 0 contains three arbitrary constants. In fact, it is not so. On dividing it by a (or b, which ever is non-zero), we get
    x + y(b/a) + (c/a),
which can be written as x + By + C = 0 where B =b/a and C = c/a.

It follows that the equation of a straight line contains two arbitrary constants, and the number of these arbitrary constants cannot be decreased further. Thus, the equation of every straight line contains two arbitrary constants, consequently, two conditions are needed to determine the equation of a straight line uniquely.

One condition yields a linear relation among two arbitrary constants and hence each arbitrary constant determines the other. Therefore, the lines which satisfy one condition contain a single arbitrary constant. Such a system of lines is called one parameter family of lines and the unknown arbitrary constant is called the parameter.

Examples of one parameter families

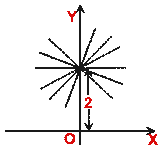
1. The equation y = m x +2, for different real values of m, represents a family of lines with y-intercept 2 units. A few members of this family are shown in figure below.
                            
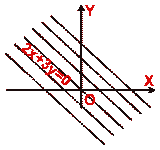
2. The equation 2 x +3 y + k = 0, for different real values of k, represents a family of lines with slope -2/3.A few members of this family are shown in figure below.
                       
3. The equation y -y₁ = m (x -x₁), for different real values of m, represents a family of lines which pass through the fixed point (x₁, y₁) except the vertical line x = x₁.
4. The equation x = a, for different real values of a, represents the family of lines parallel to y-axis (including the y-axis itself).
5. The equation a x +b y +k = 0, for different real values of k, represents a family of lines parallel to the line ax +by +c = 0.
6. The equation b x -a y +k = 0, for different real values of k, represents a family of lines perpendicular to the line ax +by +c = 0.
7. If l₁ = a₁ x +b₁ y +c₁ = 0 and l₂ = a₂ x +b₂ y +c₂ = 0 then l₁ +k l₂ = 0, for different real values of k, represents a family of lines passing through the point of intersection of the lines l₁ and l₂.

Illustrative Examples

Example

Find the equation of the family of lines with x-intercept -4.

Solution

Since the x-intercept of the family is given to be -4, therefore, each member of the family passes through the point (-4, 0).By using point-slope form, the equation of such a family of lines is y -0 = m (x -(-4)) i.e. y = m (x +4), where m is a parameter.

Note. The above equation of the family does not give the vertical line through the point (-4, 0). However, the equation of this line is x = -4 i.e. x +4 = 0.

Example

Find the equation of the straight line which is parallel to 3 x -7 y = 11 and makes x-intercept 3 units.

Solution

The given line is 3x -7 y -11 = 0 ...(i)
The equation of the family of lines parallel to (i) is
   3 x -7 y+k = 0 ...(ii) where k is a parameter.
To find x-intercept, put y = 0, we get 3 x +k = 0  =>  x =k/3
For the required member of the family which makes x-intercept 3 units,
   k/3 = 3 =>   k = -9
Substituting this value of k in (ii), the equation of the required line is
    3 x -7 y -9 = 0

Exercise

1. Write the equations of the family of lines:
   (i) with y-intercept -3
   (ii) with slope 2
   (iii) parallel to 2 x +3 +3 y -5 = 0
   (iv) perpendicular to 3 x +7 +7 y = 8
2. Find the equation of the line through the intersection of the lines 4 x -3 y +7 = 0 and 2 x +3 y +5 = 0 and the point (-4, 5).
3. Find the equation of the straight line parallel to 2 x -5 y +3 = 0 and having x-intercept -4.
4. Find the equations of two straight lines which are parallel to the line x +7 y +2 = 0 and at a unit distance from the point (2, -1).
5. Find the equations of straight lines which are perpendicular to the line 3 x +4 y -7 = 0 and are at a distance of 3 units from (2, 3).
6. Find the equations of the two straight lines drawn through the point (0, a) on which the perpendiculars dropped from the point (2 a, 2) are each of length a.
7. Find the equation of the line which lies mid-way between the lines 2 x +3 y +7 = 0 and 2 x +3 y +5 = 0.
8. Find the equations of straight lines parallel to the lines 3 x - y -3 = 0 and 3 x - y +5 = 0 and whose distances from these lines are in the ratio 3 : 5. Point out the line which lies between the given lines.
9. Find the equation of a straight line parallel to 2 x +3 y = 10 and which is such that the sum of its intercepts on the axes is 15.
10. A line is drawn perpendicular to 5 x = y +7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 5 sq. units.

Answers

1. (i) y = m x -3, m parameter                 (ii) y = 2 x +c, c parameter
   (iii) 2x + 3 + 3y + k = 0, k parameter    (iv) 7 x -3 y + k = 0, k parameter
2. 8 x +3 +3 y +17 = 0                             3. 2 x-5 y +8 = 0
4. x +7 y +5 +5 (2 +1) = 0, x +7 y -5 (2 -1) = 0
5. 4 x -3 y +16 = 0, 4x + 16 = 0, 4 x -3 y -14 = 0
6. y -a = 0, 4 x -3 y +3 +3 a = 0
7. 2 x +3 +3 y +6 = 0
8. 3 x - y = 0, 3 x - y -15 = 0 ; 3 x - y = 0
9. 2 x +3 +3 y -18 = 0
10. x +5 y -5 2 = 0, x +5 y +52 = 0