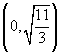Point and Circle

Let S be a circle with center C and radius r (> 0) and P be any point in the plane of the circle S, then

1. P is called exterior to S iff | C P | > r,
2. P is called interior to S iff |CP| < r and
3. P is said to lie on S iff |CP| = r.

If P is exterior to S then we say that P lies outside S, and if P is interior to S then we say that P lies inside S

Notation. Let S = x² + y² +2 g x +2 f y + c = 0, g² + f² - c > 0, be a circle and P (x₁, y₁) be a point in the plane of S, then S₁ = x₁² +y₁² +2 g x₁ +2 f y₁ + c.

Let S be a circle and P (x₁, y₁) be a point in the plane of S, then

1. P is exterior to S iff S₁ > 0
2. P is interior to S iff S₁ < 0
3. P lies on S iff S₁ = 0

Corollary.

Let S be a circle and P (x₁, y₁), Q (x₂, y₂) be two points in the plane of S then they lie

1. on the same side of S iff S₁ and S₂ have same sign
2. on the opposite sides of S iff S₁ and S₂ have opposite signs.

Exercise

1. Among the points given below, point out which of these are interior, exterior or lie on the circle S with center (1, 2) and radius 3?
   (i) (2, 3)           (ii) (-1, -3)         (iii) (4, 2)
2. Among the points given below, point out which of these are exterior, interior or lie on the circle 3 x 2 +3 y 2 -2 x -11 = 0?
   (i) (-1, 0)              (ii) (1, -2)                (iii)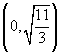
3. Do the following pairs of points lie on the same side or on opposite sides of the circle with center (- 1, 2) and radius?
   (i) (2, -3) and (1, 2)      (ii) (0, 4) and (1, 3)

Answers