Position of two Points relative to a Line

The points P (x₁, y₁) and Q (x₂ , y₂) lie on the same side or on opposite sides of the line a x +b y +c = 0 according as the expressions a x₁ + b y₁ +c and a x₂ + by₂ +c have same sign or opposite signs.

Illustrative Examples

Example

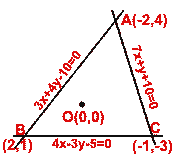
The sides of a triangle are given by the equations 3 x +4 y = 10, 4 x -3 y = 5 and 7 x +y +10 = 0. Show that the origin lies with in the triangle.
                                       .

Solution

The given lines are
3 x +4 y -10 = 0            ...(i)
4 x -3 y -5 = 0               ...(ii)
and 7 x + y +10 = 0       ...(iii)
Let ABC be the triangle formed by these lines.
Solving these equations simultaneously, taking two at a time, the vertices of the triangle are
A (-2, 4), B (2, 1) and C (-1, -3)
On substituting (-2, 4) in L.H.S. of (ii), we get -8 -12 -5 = -25
and substituting (0, 0) in L.H.S. of (ii), we get 0 -0 -5 = -5
Since both have same sign, therefore, origin and A lie on the same side of BC.
Similarly origin and B lie on the same side of CA; and origin and C lie on the same side of AB. (Please check it)
From these results, it follows that the origin lies with in the triangle formed by the given lines.

Exercise

1. Are the points (2, 3) and (-1, 5) on the same side or on opposite sides of the line y = 2 x +5.
2. Show that the points (3, 5) and (-3, -2)lie on the same side of the line 3 x = 7 y + 8.
3. Which of the points (1, 1), (-1, 2), (2, 3) and (-3, 0) lie on the same side of the line 4 x +3 y = 5 on which the origin lies?
4. Find by calculation whether the points (13, 8), (26, -4) lie in the same, adjacent or opposite angles formed by the straight line 5 x + 6 y -112 = 0 and 10 x +11 y - 217 = 0.
5. Prove that the point P (x₁, y₁) and the origin lie on the same side or on opposite sides of the line ax +by +c = 0 according as ax₁ + by₁ + c and c have same sign or opposite signs.

Answers