Practical use of Trigonometry
Trigonometric knowledge can be used to estimate heights of objects or
distances betweens points, for example, height of a mountain or breadth of a river.
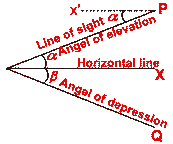
Angles of elevation and depression
If a horizontal line is drawn from the eye of the observer (O), and an
object P is above this line OX, then  POX is
called angle of elevation. If an object Q is below the horizontal line OX,
then
POX is
called angle of elevation. If an object Q is below the horizontal line OX,
then  QOX is called
angle of depression. Note that from P, the point O is situated at an angle of
depression =
QOX is called
angle of depression. Note that from P, the point O is situated at an angle of
depression =  X'PO =
X'PO =
 POX =
POX =

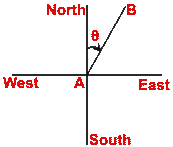
Bearings of a point
The bearing of a line in horizontal plane is the angle made by it from
North-South line. The angle (measured from north in clockwise direction) is
generally given in three figures (e.g. 045° instead of 45°). So this kind of
measurement is called three figure bearing.

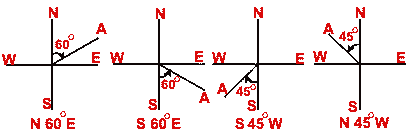
However, more frequently, quadrant bearings are used. Here, firstly
we see whether the line makes acute angle on North or South side. Then we
measure acute angle from North or South towards East or West as the case may
be, and use that measure (in degrees) and letter E or W accordingly.
Some useful figures
While solving problems on heights and distances, the following figures
should be remembered.
 2
2 1· 414,
1· 414, 3
3
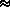 1·732,
1·732, 5
5
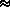 2·236
2·236
sin 0° = 0, sin 15° = ( 3 -1)/[2
3 -1)/[2 2
, sin 36° = (
2
, sin 36° = ( 5 - 1)/[2
5 - 1)/[2 2]
2]
sin 18° = ( 5 -1)/4, sin 30° = 1/2,
sin 60° = (
5 -1)/4, sin 30° = 1/2,
sin 60° = ( 3)/2 ,sin 75° = (
3)/2 ,sin 75° = ( 3
-1)/2
3
-1)/2 2
2
sin 90° = 1
Illustrative Examples
Example
A tree casts shadow
 3 times its height. Find the
angle of elevation of the sun.
3 times its height. Find the
angle of elevation of the sun.
Solution
Let BC = h be the height of the tree, so that length of shadow, AB =
 3 h. If
3 h. If
 is the angle of the elevation of
the sun, we see from the diagram that
is the angle of the elevation of
the sun, we see from the diagram that
tan  = BC/AB = h/[h
= BC/AB = h/[h 3]
= 1/
3]
= 1/ 3 = tan 30°
3 = tan 30°

 = 30°
= 30°
Example
From the top of a tower 60 m high, the angles of depression
of the top and bottom of a building are observed to be 30° and 60°
respectively. Find the height of the building. Also find the distance between
the tower and the building.
Solution
Let AB be the building h meters high, and PQ be the tower 60 m high
situated at distance BQ = x meters away.
Then AC = BQ = x, CQ = AB = h,
PC = 60 -h
From  BPQ, cot 60° = BQ/PQ = x/60
BPQ, cot 60° = BQ/PQ = x/60
=> x = 60 cot 60°
From  APC, cot 30° = AC/PC = x/(60 -h)
APC, cot 30° = AC/PC = x/(60 -h)
=> 60 -h = x/ cot 30° = 60 cot 60° tan 30° =
60 (1/ 3)(1/
3)(1/ 3) = 20
3) = 20
=> h = 60 -20 = 40
Thus the building is 40 meters high and is situated 34·64 meters away from the tower.
Example
Two boats leave a place at the same time. One travels 56 km
in the direction N 50° E, while the other travels 48 km in the direction S 80°
E. What is the distance between the boats?

Solution
Let points A and B represent the position of two boats. We have to find AB,
and we know that OA = 56 km, OB = 48 km,
 AOB = 180° -50° -80° = 50°
AOB = 180° -50° -80° = 50°
Using cosine formula in  OAB, we get
OAB, we get
cos 50° =[ (56)²+(48)² - (AB)²]/[ 2(56)(48)]
AB² = (56)² +(48)² -2 (56)(48) cos 50°
= 3136 +2304 -5376 x 0·6424
= 5440 -3455·69 = 1984·31
=> AB =  198.31 = 44·54 meters
198.31 = 44·54 meters
Example
A radio transmitter antenna of height h stands at the top
of a tall building. At a point on the ground, the angle of elevation of the
bottom of the antenna is  and that
of the top of the antenna is
and that
of the top of the antenna is  . Prove
that the height of the building is h tan
. Prove
that the height of the building is h tan
 /(tan
/(tan -tan
-tan ).
).
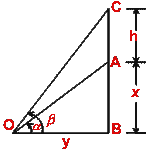
Solution
Let AB be the building of height x, CA be the antenna of height h, and y be
the distance of the observer from the foot of the building.
In  OBC, tan
OBC, tan = (x +h)/y
= (x +h)/y
In  OAB, tan
OAB, tan = x/y
= x/y
Eliminating y between these two equations,
(x +h)/x = tan  / tan
/ tan =>
x tan
=>
x tan +h tan
+h tan =
x tan
=
x tan
=> h tan = x tan
= x tan -x tan
-x tan
=> x = h tan /(tan
/(tan -tan
-tan )
)
Exercise
- A kite with a string 150 ft. makes an angle of 45° with the ground.
Assuming that the string is straight, how high is the kite?
- A tree 10 meters high casts a 17·3 meter shadow. Find the angle of
elevation of the sun.
- From the top of a hill, the angles of depression of two consecutive
kilometre stones due east are 30 and 45 degrees. How high is the hill?
- A 12 meter ladder is inclined to the vertical at angle 15°. How far is it
from the base?
- An observer in a lighthouse is 66 feet above the surface of the water.
The observer sees a ship and finds the angle of depression to be 0·7°.
Estimate the distance of the ship from the base of the lighthouse. Round the
answer to the nearest 5 feet.
- From the point on a ground level, you measure the angle of elevation to
the top of a mountain to be 45°. Then you walk 200 m further away from the
mountain and find that the angle of elevation is now 30°. Find the height of
the mountain. Round the answer to the nearest meter.
- A surveyor stands 30 yards from the base of a building. On top of the
building is a vertical radio antenna. Let
 denote the angle of elevation when
the surveyor sights to the top of the building. Let
denote the angle of elevation when
the surveyor sights to the top of the building. Let
 denote the angle of elevation when
the surveyor sights to the top of the antenna. Express the length of the
antenna in terms of the angles
denote the angle of elevation when
the surveyor sights to the top of the antenna. Express the length of the
antenna in terms of the angles  and
and
 .
.
- A helicopter hovers 800 feet directly above a small island. From the
helicopter, the pilot takes a sighting to a point directly ashore on the
mainland, at the waters edge. If the angle of depression is 30°, how far off
the coast is the island?
- A ladder 18 feet long leans against a building. The ladder forms an angle
of 60° with the ground.
(i) How high up the side of the building does the ladder reach?
(ii) Find the horizontal distance from the foot of the ladder to the base of the building.
- Two satellite tracking stations, located at points A and B in a desert,
are 200 miles apart. At a prearranged time, both stations measure the angle
of elevation of a satellite as it crosses the vertical plane containing A and
B. If the angles of elevation from A and from B are
 and
and  respectively, express the
altitude h of the satellite in terms of
respectively, express the
altitude h of the satellite in terms of
 and
and
 .
.
- From the base of a 30 m high building, the angle of elevation of a tower
is 60°, and from the top of the building, it is 30°.Find the height of the tower.
- A man on the top a building 30 meters high observes a man coming directly
towards it at a uniform speed. If it takes 15 minutes for the angle of
depression to change from 30° to 45°, how much time will it take after this
for the man to reach the base of the building? Round your answer to nearest minute.
- An aeroplane flying horizontally 1 km above the ground is observed at an
elevation of 60°.If after 10 seconds, the elevation is observed to be 30°,
find the uniform speed per hour of the plane.
- A man standing south of a lamppost observes his shadow on the horizontal
plane to be 24 ft long. On walking eastwards 300 ft, he finds his shadow as
30 ft. If his height is 6 ft, find the height of the lamp above the plane.
- Two poles of equal height are standing opposite to each other on either
side of a road, which is 30 ft wide. From a point between them on the road,
the angles of elevation of the tops are 30° and 60°. Find the height of each
pole, rounded to nearest feet.
- A vertical tower is surmounted by a vertical flagstaff of height 10 ft.
At a point on the plane, the angles of elevation of the bottom and the top of
the flagstaff are
 and
and
 respectively. Prove that the
height of the tower is 10 tan
respectively. Prove that the
height of the tower is 10 tan  /(tan
/(tan -tan
-tan ) feet.
) feet.
- An aeroplane when 6000 m high passes vertically above another plane at an
instant when their angles of elevation at the same observing point are 60°
and 45° respectively. How many meters higher is the one than the other?
- At the foot of a mountain, the elevation of its peak is 45°. After
ascending 100 m towards the mountain up a slope of 30° inclination, the
elevation is found to be 60°. Find the height of the mountain (to the nearest meter).
- A vertical pole is struck by a speeding car and breaks into two, the top
striking the ground at an angle of 30° and at a distance of 10 feet from the
foot of the pole. Find the total height of the pole.
- The breadth of a street between two houses is 9 meters and the angle of
depression of the top of one, as observed from the top of the other, which is
12 meters high, is 30°. Find the height of the other house.
- A town B is 13 km south and 18 km west of town A. Find the bearing and distance of B from A.
Answers
1. 75 2 ft
2. Approx 30°
3. 2·37 km
2 ft
2. Approx 30°
3. 2·37 km
4. 3·10 m
5. 5400 ft
6. 273·22 m
7. 30 (tan -tan
-tan )
8. 800
)
8. 800 3m
3m
9. (i) 9 3 ft (ii) 9 ft
10. 200 /(cot
3 ft (ii) 9 ft
10. 200 /(cot -cot
-cot ) miles
) miles
11. 45 m
12. 41 minutes
13. 240  3 km/hr
3 km/hr
14. 106 ft
15. 13 feet
17. 2536 m
18. 137 m
19. 17·32 ft
20. 6·8 m
21. 22·2 km, S 54°10' W

![]() POX is
called angle of elevation. If an object Q is below the horizontal line OX,
then
POX is
called angle of elevation. If an object Q is below the horizontal line OX,
then ![]() QOX is called
angle of depression. Note that from P, the point O is situated at an angle of
depression =
QOX is called
angle of depression. Note that from P, the point O is situated at an angle of
depression = ![]() X'PO =
X'PO =
![]() POX =
POX =
![]()




![]() 2
2![]() 1· 414,
1· 414,![]() 3
3
![]() 1·732,
1·732,![]() 5
5
![]() 2·236
2·236![]() 3 -1)/[2
3 -1)/[2![]() 2
, sin 36° = (
2
, sin 36° = (![]() 5 - 1)/[2
5 - 1)/[2![]() 2]
2]![]() 5 -1)/4, sin 30° = 1/2,
sin 60° = (
5 -1)/4, sin 30° = 1/2,
sin 60° = (![]() 3)/2 ,sin 75° = (
3)/2 ,sin 75° = (![]() 3
-1)/2
3
-1)/2![]() 2
2![]() 3 times its height. Find the
angle of elevation of the sun.
3 times its height. Find the
angle of elevation of the sun.![]() 3 h. If
3 h. If
![]() is the angle of the elevation of
the sun, we see from the diagram that
is the angle of the elevation of
the sun, we see from the diagram that![]() = BC/AB = h/[h
= BC/AB = h/[h![]() 3]
= 1/
3]
= 1/![]() 3 = tan 30°
3 = tan 30°![]()
![]() = 30°
= 30°

![]() BPQ, cot 60° = BQ/PQ = x/60
BPQ, cot 60° = BQ/PQ = x/60![]() APC, cot 30° = AC/PC = x/(60 -h)
APC, cot 30° = AC/PC = x/(60 -h)![]() 3)(1/
3)(1/![]() 3) = 20
3) = 20

![]() AOB = 180° -50° -80° = 50°
AOB = 180° -50° -80° = 50°![]() OAB, we get
OAB, we get![]() 198.31 = 44·54 meters
198.31 = 44·54 meters![]() and that
of the top of the antenna is
and that
of the top of the antenna is ![]() . Prove
that the height of the building is h tan
. Prove
that the height of the building is h tan
![]() /(tan
/(tan![]() -tan
-tan![]() ).
).
![]() OBC, tan
OBC, tan![]() = (x +h)/y
= (x +h)/y![]() OAB, tan
OAB, tan![]() = x/y
= x/y![]() / tan
/ tan![]() =>
x tan
=>
x tan![]() +h tan
+h tan![]() =
x tan
=
x tan![]()
![]() = x tan
= x tan![]() -x tan
-x tan![]()
![]() /(tan
/(tan![]() -tan
-tan![]() )
)