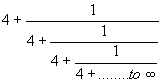Solving Quadratic Equations by Formula
The roots of the equation a x² +b x +c = 0, a  0 are
0 are
[-b +  (b² -4ac)]/2a,
[-b -
(b² -4ac)]/2a,
[-b -  (b² -4ac)]/2a
(b² -4ac)]/2a
Thus a quadratic equation has exactly two roots: equal or distinct; real or imaginary.
Remarks
- If a quadratic equation in a variable x is satisfied by more than two
values of x, then it will be satisfied by all values of x and hence it is an identity.
- If the coefficients of quadratic are rational, and one of the roots is
irrational, then the other root is its conjugate.
- If the quadratic equation has real coefficients, then if the roots are
complex numbers, they occur in conjugate pair.
Illustrative Examples
Example
Solve: 22x +8 +1 = 32. 2x.
Solution
Given 22x +8+1 = 32. 2x => 28.22x
+1 = 32. 2x
=> 256. (2x)² -32. 2x +1 = 0
Putting 2x = t, we get, 256 t² -32t +1 = 0
=> t = [-(-32) + (- 32)² -4 (256)(1)]/[2 (256)] =
(32 ± 0)/512 = 1/16, 1/16
(- 32)² -4 (256)(1)]/[2 (256)] =
(32 ± 0)/512 = 1/16, 1/16
But t = 2x. Hence 2x = t = 1, 1 = 2-4, 2-4
=> x = -4, -4
Hence the solution of the given equation is x = -4
Example
Solve (x +1)(x +2)(x +3)(x +4) = 120.
Solution
If the problem has four factors (x +a)(x +b)(x +c)(x +d), and the sum of
two of the numbers a, b, c, d is equal to the sum of the other two, then we
make the substitution as under:
(x +1)(x +2)(x +3)(x +4) = 120
=> [(x +1)(x +4)] [(x +2)(x +3)] = 120
=> (x² +5 x +4)(x² +5 x +6) = 120
Putting y = x² +5 x, we get
(y +4)(y +6) = 120 => y² +10 y +24 = 120
=> y² +10 y -96 = 0 => y = [- 10 ±  [(10)² -4
(1)(-96)]]/[2(1)]
[(10)² -4
(1)(-96)]]/[2(1)]
=> y = (-10 ±  484)/2 = (- 10 ± 22)/2 = 6, -16
484)/2 = (- 10 ± 22)/2 = 6, -16
When y = 6, we get x² +5 x = 6
=> x² +5 x -6 = 0 => (x -1)(x +6) = 0
=> x = 1, -6.
When y = -16, we get x² +5x = -16 => x² +5x +16 = 0
=> x = [-5 ±  [(5)² -4 (1)(16)]]/[2 (1)] = (-5 ±
[(5)² -4 (1)(16)]]/[2 (1)] = (-5 ±
 -39)/2 = (-5 ± i
-39)/2 = (-5 ± i  39)/2
39)/2
Hence the required solutions are 1, -6, (-5 ±i  39)/2
39)/2
Example
- Evaluate
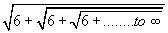
- If 3 =
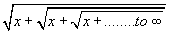 ,
find x.
,
find x.
- Evaluate the continued fraction
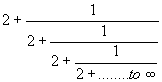
Solution
- Let x =
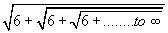
Squaring both sides, we get
x² = 6 +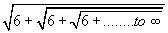 = 6 +x
= 6 +x
=> x² -x -6 = 0 => (x -3)(x +2) = 0 => x = 3, -2
As the value of given expression should be positive, we ignore x = -2. Hence
the value of the given expression is 3.
- We are given that 3 =
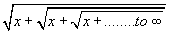
Squaring both sides, we get
9 = x +
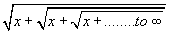 = x +3
= x +3
=> x = 6
- Let x =
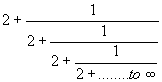
Then x = 2 +1/x => x² = 2 x +1 => x² -2 x -1 = 0
=> x = [-(-2) ±  (-2)² -4 (1)(-1)]/[2(1)] = (2 ±
(-2)² -4 (1)(-1)]/[2(1)] = (2 ±
 8)/2
8)/2
= (2 ± 2
 2)/2 = 1 ±
2)/2 = 1 ± 2
2
But the given expression is positive. Hence the value of the given continued
fraction is 1 ± 2.
2.
Example
Solve the equation  (2x +7) +
(2x +7) + (3x
-18) =
(3x
-18) =  (7x +1).
(7x +1).
Solution
Squaring both sides of the given equation, we get
2x +7 +3x -18 +2  (2x +7).
(2x +7).  (3x -18)
= 7 x +1
(3x -18)
= 7 x +1
=> 2  (2x +7).
(2x +7). (3x -18)
= 2 x +12
(3x -18)
= 2 x +12
=>  (2x +7).
(2x +7). (3x -18)
= x +6
(3x -18)
= x +6
Squaring, (2x +7)(3x -18) = (x +6)²
=> 6x² -15x -126 = x² +12 x +36
=> 5x² - 27x -162 = 0
=> (5x +18)(x -9) = 0 => x = -18/5, 9
For x = -18/5,  (2x +7) is meaningless. Hence the only
solution is x = 9.
(2x +7) is meaningless. Hence the only
solution is x = 9.
Example
Three consecutive natural numbers are such that the square
of the middle number exceeds the difference of the squares of the other two by
60. Assume the middle number to be x and form a quadratic equation satisfying
the above statement. Hence find the three numbers.
Solution
Since the middle number of the three consecutive numbers is x, the other
two numbers are x -1 and x +1.
According to the given condition, we have
x² = [(x +1)² -(x -1)²] +60
=> x² = (x² +2x +1) -(x² -2x +1) +60 = 4x +60
=> x² -4x -60 = 0 => (x -10)(x +6) = 0
=> x = 10 or -6
Since x is a natural number, we get x = 10
Hence the three numbers are 9, 10, 11
Example
Determine all values of x for which
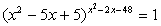
Solution
We know that ab = 1 if b = 0, a 0 or if a = 1
0 or if a = 1
Given that 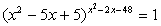
Now x² -2x -48 = 0 => (x -8)(x +6) = 0 => x = 8, -6
Also for x = 8 or -6, base = x² -5 x +5  0
0
x² -5x +5 = 1 => x² -5x +4 = 0
=> (x -1)(x -4) = 0 => x = 1, 4
Hence the solutions of the given equation are x = -6, 1, 4, 8
Exercise
Solve the following equations (1-9):
- (i) x4 -8x² -9 = 0
(ii) x4 -5x² +6 = 0
- (i) 3x +3-x = 2
(ii) 2x +1 +4x = 8
- (i) 5x +1 +52 +x = 5³ +1
(ii) 4x -3x+1/2 = 3x+1/2 -22x -1
- x2/3 -x1/3 -2 = 0
- (x² +3x +2)² -8(x² +3x) -4 = 0
- 1/(x + 1) - 2/(x + 2) = 3(x + 3) - 4/(x + 4)
- x(x +2)(x +3)(x +5) = 72
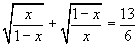
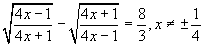
- Evaluate (i)
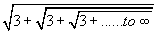
(ii) 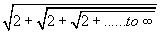
- Solve 5 =
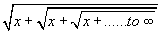
- Evaluate the continued fraction
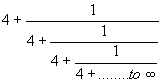
- Solve (i) x +2 =
 (2x +7)
(2x +7)
(ii)  (x +15) = x +3
(x +15) = x +3
- Solve
 (x +5) +
(x +5) +  (x +21) =
(x +21) =
 (6x +40)
(6x +40)
- The hypotenuse of a right angled triangle is 17 cm and the difference
between the other two sides is 7 cm. Find the two unknown sides.
- A trader bought a number of articles for Rs 1200. Ten were damaged and he
sold each of the rest at Rs 2 more than what he paid for, thus clearing a
profit of Rs 60 on the whole transaction. Taking the number of articles he
bought as x, form an equation in x and solve it.
- Two years ago, a mans age was three times the square of his sons age. In
three years time, his age will be four times his sons age. Find their present ages.
- The sum of two numbers is 9 and the sum of their squares is 41. Taking
one number as x, form an equation in x and solve it to find the numbers.
- A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk
of uniform width. Given that area of the walk is 120 square meters, find its width.
- An express train makes a run of 240 km at a certain speed. Another train,
whose speed is 12 km/hr less takes an hour longer to make the same trip. Find
the speed of the express train.
- A certain positive integer exceeds its square root by 20. Find the number.
- Divide 39 into 2 parts whose product is 338.
- A two digit number is four times the sum and three times the product of
its digits. Find the number.
- The sum of the squares of two consecutive positive even integers is 340.
Find the integers.
Answers
1. (i) ± 3, ±i
(ii) ± 3, ±
3, ± 2
2. (i) 0
(ii) 1
2
2. (i) 0
(ii) 1
3. (i) -1, 2
(ii) 3/2
4. -1, 8
5 . -4, -3, 0, 1
6. 0, -5/2
7. 1, -6, (-5 +i  23)/2
8. 9/13, 4/13
23)/2
8. 9/13, 4/13
9. -5/16
10. (i) (1 + 13)/2
(ii) 2
13)/2
(ii) 2
11. 20
12. 2 + 5
5
13. (i) 1
(ii) 1
14. 4
15. 8 cm, 15 cm
16. (x -10)
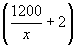 = 1200
+60; x = 100
= 1200
+60; x = 100
17. 29, 5 yrs
18. x² +(9 -x)² = 41; the numbers are 4, 5
19. 2 meters
20. 60 km/hr
21. 25
22. 26, 13
23. 24
24. 12, 14
![]() 0 are
0 are![]() (b² -4ac)]/2a,
[-b -
(b² -4ac)]/2a,
[-b - ![]() (b² -4ac)]/2a
(b² -4ac)]/2a![]() (- 32)² -4 (256)(1)]/[2 (256)] =
(32 ± 0)/512 = 1/16, 1/16
(- 32)² -4 (256)(1)]/[2 (256)] =
(32 ± 0)/512 = 1/16, 1/16![]() [(10)² -4
(1)(-96)]]/[2(1)]
[(10)² -4
(1)(-96)]]/[2(1)]![]() 484)/2 = (- 10 ± 22)/2 = 6, -16
484)/2 = (- 10 ± 22)/2 = 6, -16![]() [(5)² -4 (1)(16)]]/[2 (1)] = (-5 ±
[(5)² -4 (1)(16)]]/[2 (1)] = (-5 ±
![]() -39)/2 = (-5 ± i
-39)/2 = (-5 ± i ![]() 39)/2
39)/2![]() 39)/2
39)/2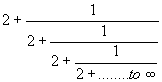
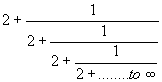
![]() (2x +7) +
(2x +7) +![]() (3x
-18) =
(3x
-18) = ![]() (7x +1).
(7x +1).![]() (2x +7).
(2x +7). ![]() (3x -18)
= 7 x +1
(3x -18)
= 7 x +1![]() (2x +7).
(2x +7).![]() (3x -18)
= 2 x +12
(3x -18)
= 2 x +12![]() (2x +7).
(2x +7).![]() (3x -18)
= x +6
(3x -18)
= x +6![]() (2x +7) is meaningless. Hence the only
solution is x = 9.
(2x +7) is meaningless. Hence the only
solution is x = 9.![]()
![]() 0 or if a = 1
0 or if a = 1![]()
![]() 0
0