Quadratic Inequations
Inequations of the type a x² +b x +c > 0, a x² + b x +c 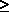 0,
a x² +b x +c < 0, a x² +b x +c
0,
a x² +b x +c < 0, a x² +b x +c  0 (a
0 (a 0)
are called quadratic inequalities.
0)
are called quadratic inequalities.
Solving Quadratic Inequalities
First make the coefficient of x² unity by multiplying throughout by 1/a,
and reversing the inequality sign if a is negative. Now, three cases arise:
Case I. If the quadratic has real distinct roots, say
 ,
,  and
and  <
<  , then
, then
- (x -
 )(x -
)(x - ) > 0
=> x <
) > 0
=> x <  or x >
or x > 
- (x -
 (x -
(x - )
) 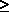 0 => x
0 => x 
 or
x
or
x 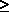

- (x -
 )(x -
)(x - ) < 0
=>
) < 0
=>  < x <
< x < 
- (x -
 )(x -
)(x - )
)  0 =>
0 => 
 x
x 

Case II. If the quadratic has two real, identical roots say
 ,
,  , then we know that x²
, then we know that x²
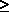 0 for real x. Therefore
0 for real x. Therefore
- (x -
 )²
)² 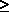 0 =>
x
0 =>
x  R (all real numbers)
R (all real numbers)
- (x -
 )² > 0 => x
)² > 0 => x  R except x =
R except x = 
- (x -
 )²
)²  0 =>
x =
0 =>
x = 
- (x -
 )² < 0
=> there is no solution.
)² < 0
=> there is no solution.
Case III. If the quadratic has complex roots, then either there is
no solution or the entire set of real numbers is the solution.
Sign of Quadratic expressions
- a x² +b x +c has same sign as a except when a x² +b x +c = 0 has two real
and distinct roots, say
 ,
,  (
( <
<  ) and
) and  < x <
< x <  .
.
- a x² +b x +c is +ve for all real x, when a > 0 and
 < 0.
< 0.
- a x² +b x +c is -ve for all real x, when a < 0 and
 < 0.
< 0.
Range (Maximum / Minimum Value) of Quadratic Expressions
Hence the maxima / minima occurs at x = -b/2a and is equal to -
 /4a. If a > 0, we have a minima, otherwise we have a
maxima.
/4a. If a > 0, we have a minima, otherwise we have a
maxima.
Illustrative Examples
Example
Solve algebraically:
- 2 x² +x -1 < 0
- x² +2x +3
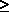 0
0
- x² +x +1 < 0
Solution
- 2 x² +x -1 < 0 => (x +1)(2 x -1) < 0
=> (x +1)(x -1/2) < 0
(Dividing by 2)
=> -1 < x < 1/2, which is the required solution.
We can also write it as x  (-1, 1/2)
(-1, 1/2)
- For x² +2 x +3
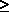 0, the discriminant
0, the discriminant
 = 2² -4.1.3 = -8 < 0, so roots are complex.
= 2² -4.1.3 = -8 < 0, so roots are complex.
Now x² +2 x +3 = (x +1)² +2 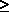 2 for all real x.
2 for all real x.
Hence x² +2 x +3 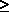 0 is true for all real x.
0 is true for all real x.
- For x² +x +1 < 0, discriminant
 = 1² -4.1.1 = -3 < 0, so roots are complex.
= 1² -4.1.1 = -3 < 0, so roots are complex.
Now 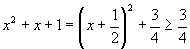 for all real x.
for all real x.
So x² +x +1 < 0 has no solution.
Exercise
- Discuss the sign of x² -3 x +2.
- Solve the following inequalities:
(i) -x² +3 x -2 > 0
(ii) 4 x² -9 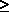 0
0
(iii) 2 x² +x -15 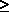 0.
0.
- Solve the following inequalities:
(i) 2 x² < x
(ii) 3 -2 x²> 5 x
(iii) x² -6 x +19 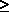 0
(iv) x² -6 x +11 < 1.
0
(iv) x² -6 x +11 < 1.
- Find all real values of x which satisfy x² -3 x +2 > 0 and x² -3 x
-4
 0.
0.
- Find the range of x for which 6 +x < 2 x².
- If x is real, prove that 5 x² -8 x +6 is always positive and find its minimum value.
- If x be real, find the maximum value of a² +2 a x - x².
- Find the values of a so that expression x² -(a +2) x +4 is always positive.
- Construct a quadratic polynomial which is zero when x = 3, 5 and whose
minimum value is -1. How many such polynomials are possible?
- Can you construct a quadratic polynomial which is zero when x = 3, 5 and
whose maximum value is
(i) 2
(ii) -2?
- Solve: log2 (x² -1) = 3.
- Write the most general quadratic expression whose
(i) minimum value is K
(ii) maximum value is K.
Answers
1. -ve when 1 < x < 2, zero at x = 1, 2; +ve otherwise.
2. (i)  (1, 2)
(ii) x > 3/2 or x < -3/2
(1, 2)
(ii) x > 3/2 or x < -3/2
(iii) 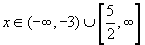
3. (i) 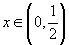 (ii) -3 < x < 1/2
(iii) all real values of x
(ii) -3 < x < 1/2
(iii) all real values of x
(v) no real value of x.
4. -1  x < 1 or 2 < x
x < 1 or 2 < x  4.
4.
5. x < -3/2 or x > 2.
6. 14/5
7. 2a² at x = a.
8. -6 < a < 2.
9. x² -8 x +15; only one.
10. (i) Yes, -2 x² +16 x -30 (ii) No.
11. -3  x < -1 or 1 < x
x < -1 or 1 < x  3.
3.
12. (i) (a x +b)² +K
(ii) K -(a x +b)²
![]() 0,
a x² +b x +c < 0, a x² +b x +c
0,
a x² +b x +c < 0, a x² +b x +c ![]() 0 (a
0 (a![]() 0)
are called quadratic inequalities.
0)
are called quadratic inequalities.![]() ,
, ![]() and
and ![]() <
< ![]() , then
, then![]() ,
, ![]() , then we know that x²
, then we know that x²
![]() 0 for real x. Therefore
0 for real x. Therefore![]() /4a. If a > 0, we have a minima, otherwise we have a
maxima.
/4a. If a > 0, we have a minima, otherwise we have a
maxima.