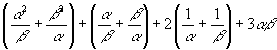Relations between Roots and Coefficients

Formulae

Sum and product of roots
Sum of roots = + = - b/a = - (coefficient of x)/(coefficient of x²)
Product of roots = = c/a = (constant term)/(coefficient of x²)

Symmetric functions of roots

From + = -b/a and = c/a, values of other functions of and can be calculated:
( - )² = ( + )² -4 ,
² + ² = ( + )² -2 ,
³ + ³ = ( + )³ -3 ( + ),
4 + 4 = [( + )² -2 ]² -2 ( )²,
² - ² = ( + )( - ) etc.

Formation of a quadratic equation with given roots

x² -S x +P = 0, where S = sum of roots and P = product of roots.

Illustrative Examples

Example

If , are roots of the equation x² -4 x +2 = 0, find the values of

  1. ² + ²
  2. ² - ²
  3. ³ + ³
  4. 1/ + 1/

Solution

As , are roots of the equation x² -4 x +2 = 0,
      + = -(-4)/1 = 4, = 2/1  = 2

  1. ² +² = ( + )² -2 = (4)² -2 (2) = 12
  2. ² -² = ( + )( -).
        Now ( -)² = ( +)² -4 = (4)² -4 (2) = 8
         - = ± 8 = ±2 2
        ² -² = ( +)( -) = (4)(±2) = ±8
  3. ³ +³ = ( +)³ -3 ( +)
        = (4)³ -3 (2)(4) = 64 -24
        = 40
  4. 1/ + 1/ = ( + )/ = 4/2 =2

Example

If , are roots of the quadratic equation ax² +bx +c = 0, form an equation whose roots are

  1. - , -
  2. 1/, 1/

Solution

Since , are roots of a x 2 +b x +c = 0,
                + = -b/a, = c/a

  1. Here, S = (-) +(-) = -( + ) = -(-b)/a = b/a
    P = (- )(-) = = c/a
    Hence the required equation is x² -S x +P = 0
    i.e. x² - (b/a) x + c/a = 0 i.e. a x² -b x +c = 0
  2. Here, S = 1/ + 1/ = ( +)/ = - (b / a)/(c / a) = - b/c
    P = (1/).(1/) = 1/( ) = 1/(c/a) = a/c
    Hence the required equation is x² -S x +P = 0
    i.e. x² -(- b/c) x + a/c = 0 i.e. cx² +bx +a = 0

Example

Find p, q if p and q are roots of the equation x² +px +q = 0.

Solution

Since p, q are roots of x² +px +q = 0, p +q = -p and pq = q.
Now pq = q => pq -q = 0 => q(p -1) = 0 => q = 0 or p = 1.
When q = 0 then p +q = -p => 2p = -q = 0 => p = 0.
When p = 1, then p +q = -p => q = -2 p = -2.
Hence the required solutions are p = q = 0 or p = 1, q = -2.

Example

If the roots of the equation 2 x² +(k +1) x +(k² -5 k +6) = 0 are of opposite signs then show that 2 < k < 3.

Solution

Since roots are of opposite signs, roots are real and distinct,
    discriminant> 0 and product of roots < 0
(k +1)² -4. 2. (k² -5 k +6) > 0 and (k² -5 k +6)/2 < 0
First condition is always true when second holds.  (because (k +1)² = 0)
Hence (k² -5 k +6)/2 < 0    =>   k² -5 k +6 < 0    =>   (k -2)(k -3) < 0
=>   2 < k < 3

Example

The coefficient of x in the equation x² +p x +q = 0 was taken as 17 in place of 13 and thus its roots were found to be -2 and -15. Find the roots of the original equation.

Solution

By given conditions, -2 and -15 are roots of the equation x² +17 x +q = 0
Hence product of roots = (-2)(-15) = q/1 => q = 30.
Therefore, the original equation is x² +13 x +30 = 0
=>   (x +10)(x +3) = 0      =>   x = -3, -10
Hence the roots of the original equation are -3, -10.

Exercise

  1. Write the sum and product of the roots of the following equations:
    (i) x² +9 = 0
    (ii) 2 x² -2 x +4 = 0.
  2. If , are the roots of the equation 3 x² -6 x +4 = 0, evaluate
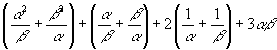
  3. If the roots of the equation x² +p x +7 = 0 are denoted by and , and ² +² = 22, find the possible values of p.
  4. If , be the roots of the equation a x² +b x +c = 0, find the value of
    (i) ² + ²
    (ii) / + /
    (iii) ³ + ³
    (iv) | -
    (v) ² - ²
    (vi) 6 + 6
  5. If , are roots of x² +k x +12 = 0 and - = 1, find k.
  6. The sum of the roots of the equation 1/(x+a) + 1/(x+b) = 1/c is zero.
    Prove that the product of the roots is - (a² +b²)/2
    [Hint. Rewrite the equation as x² +x (a +b -2 c) +(ab -bc -ca) = 0.]
  7. Two candidates attempt to solve a quadratic equation of the form x² +p x +q = 0. One starts with a wrong value of p and finds the roots to be 2 and 6. The other starts with a wrong value of q and finds the roots to be 2 and -9. Find the correct roots and the equation.
  8. Given that and are the roots of the equation x² = 7 x +4,
    (i) Show that ³ = 53 +28
    (ii) Find the value of / + /
  9. Form an equation whose roots are
    (i) 3, -1/3
    (ii) 3, 1/3
    (iii) 0, 0
  10. Form an equation with rational coefficients one of whose roots is
    (3 +1)/(3 -1)
  11. Form an equation with real coefficients one of whose roots is
    (i) -1 -2 i
    (ii) -2 --3
    (iii) 1/(2 + -2)
  12. If , are the roots of the equation a x² +b x +c = 0, then form an equation whose roots are:
    (i) 2, 2
    (ii) /2, /2
    (iii) / , /
    (iv) ( +)², ( -)²
    (v) (/) +1, (/) +1
    (vi) +k, +k
  13. If , be the roots of the equation 2 x² -3 x +1 = 0, find an equation whose roots are  /(2 +3), /(2 +3)

Answers

1. (i) 0, 9        (ii) 1, 2 2    2. 8                 3. ±6
4. (i) (b² -2ac)/a²     (ii) (b² -2ac)/ac      (iii) (3a b c -b³)/a³ (iv) [ (b² -2ac)]/|a|
    (v) ± [b (b² -2ac)]/a²               (vi) [b6 +9 a² b² c² -6ab4 c -2c³ a³]/a6
5. ±7                 7. -3, -4; x² +7 x +12 = 0    8. (ii) -57/4
9.(i) 3 x² -8 x -3 = 0 (ii) 3x² -4x + 3 = 0  (iii) x² = 0
10. x² -4 x +1 = 0
11. (i) x² +2 x +5 = 0 (ii) x² +4 x +7 = 0 (iii) 6 x² -4 x +1 = 0
12. (i) a x² +2 b x +4 c = 0
     (ii) 4 a x² +2 b x +c = 0
     (iii) a c x² -(b² -2 a c) x +a c = 0
     (iv) a 4 x² -2 a² (b² -2 a c) x +b²(b² -4 ac) = 0
     (v) a c x² +b (a +c) x +(c + a)² = 0
     (vi) a x² -(2 a k -b) x +(a k² -b k +c) = 0
13. 40 x² -14 x +1 = 0