Sign, Domain and range of T-ratios

Sign of t-ratios

Quadrant	I	II	III	IV
T-ratios which are +ve	All	sin cosec	tan cot	cos sec

This table can be memorised with the help of phrase "Add Sugar To Coffee"

Add	Sugar	To	Coffee
All	Sin	Tan	Cos
I	II	III	IV

Domain of T-ratios

Function	Domain
sin, cos	all real numbers
tan, sec	all real numbers other than (2 n +1) /2, n Z
cot, cosec	all real numbers other than n , n Z

Limits of T-ratios (i.e. range)

The maximum and minimum values of sin and cos are +1 and -1 respectively.
Thus, -1 cos 1 and -1 sin 1

Function	Range
sin, cos	[-1, 1]
tan, cot	any real value
sec, cosec	any real value except (-1, 1)

Illustrative Examples

Example

If tan = -2, find the values of the remaining trigonometric ratios of .

Solution

Given tan = -2 which is - ve, therefore, lies in second or fourth quadrant.
Also sec² = 1 + tan² = 1 +(-2)² = 5
=>   sec = ±5
Two cases arise:
Case I. When lies in the second quadrant, sec is - ve.
sec = -5   =>   cos = -1/5
sin = (sin/cos).cos = tan. cos = (-2).(-1/5) = 2/5
=>   cosec = (5)/2
Also tan = -2   =>   cot = -1/2
Case II. When lies in the fourth quadrant, sec is + ve.
sec = 5    =>    cos = 1/5
sin = (sin/cos).cos = tan. cos = (-2).(1/5) = -2/5
=>  cosec = -(5)/2
Also tan = -2    =>    cot = -1/2

Example

Prove that sin = x + 1/x is not possible for real x.

Solution

When x > 0, x +1/x = (x - 1/x)² +2 2
When x < 0, let x = -y where y > 0. Then

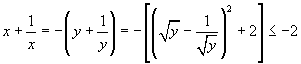
Thus x +1/x 2 or x +1/x -2
=>    sin 2   or sin -2
Also, we know that -1 sin 1
Hence sin = x +1/x is not possible for any real x.
Aliter.
sin = x +1/x =>  x 2 -sin . x +1 = 0
It is a quadratic in x. As x is real, it has real roots
=>    (-sin )² -4. 1. 1 0             (discriminant 0)
=>   sin² 4  =>    |sin | 2
=>    sin -2 or sin 2
Also we know that 1 sin -1
Hence sin = x +1/x is not possible for any real x.

Example

Is the equation 2 sin² -cos +4 = 0 possible?

Solution

2 sin² -cos +4 = 0
=>     2 (1 -cos² ) -cos +4 = 0
=>   -2 cos² +cos -6 = 0
=>   2 cos² +cos -6 = 0
=>   (2 cos -3)(cos + 2) = 0
=>   2 cos -3 = 0 or cos +2 = 0
=>    cos = 3/2 or cos = -2, both of which are impossible as -1 cos 1.
Hence the equation 2 sin² -cos +4 = 0 is not possible.

Exercise

1. Which of the six t-ratios are positive for the angles
   (i) 240°       (ii) -420°?
2. Find the other five t-ratios if
   (i) cos A = 1/2 and A lies in the second quadrant
   (ii) sin A = 3/5 and /2 < A <
   (iii) tan A = 3/2 and A does not lie in first quadrant
   (iv) cot A = 12/5 and < A < 3/2
3. In which quadrant does lie if
   (i) cos is positive and tan is negative
   (ii) both sin and cos are negative
   (iii) sin = 4/5 and cos = 3/5
   (iv) sin = 2/3 and cos = 1/3
4. For what real values of x is the equation 2 cos = x +1/x possible?
5. If sin sec = -1 and lies in the second quadrant, find sin and sec .
6. If sec A = x +1/4x, prove that sec A +tan A = 2 x or 1/2x.
7. If sin = 12/13 and lies in the second quadrant, show that
   sec +tan = -5.
8. If sin : cos : : 3 : 1, find sin , cos .

Answers

1. (i) tan, cot     (ii) cos, sec
2. (i) sin A = 3/2 , tan A = -3, cot A = -1/3, sec A = -2, cosec A = 2/3
    (ii) cos A =  4/5, tan A =   3/4, cot A =  4/3, sec A =  5/4, cosec A = 5/3
    (iii) sin A =  3/5, cos A =  4/5, cot A = 4/3, sec A =  5/4 , cosec A =  5/3
     (iv) sin A =    5/13 , cos A =  12/13, tan A = 5/12 , sec A =  13/12, cosec A = -13/5
3. (i) fourth    (ii) third       (iii) second
    (iv) not possible as we must have sin² +cos² = 1
4. x = ±1 only
5. 1/2, -2
8. sin = 3/2, cos = 1/2 or sin = - 3/2, cos = 1/2