(i) a x +b y +c < 0 (ii) a x +b y +c
(iii) a x +b y +c> 0 (iv) a x +b y +c
where a, b, c are real numbers and at least one of a and b is non-zero, is called a linear inequation (or inequality) in two variables x and y.
A statement of any one of the following types:
(i) a x +b y +c < 0
(ii) a x +b y +c ![]() 0
0
(iii) a x +b y +c> 0
(iv) a x +b y +c ![]() 0
0
where a, b, c are real numbers and at least one of a and b is non-zero, is
called a linear inequation (or inequality) in two variables x and y.
The set of all ordered pairs of real numbers which satisfy a given inequation is called the solution set of the given inequation.
Solve the inequations 3 x +2 y > 5 and x +y
![]() 1 simultaneously.
1 simultaneously.
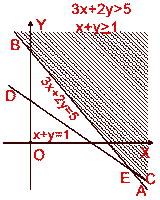
The given inequations are
3 x +2 y > 5 ... (i)
and x +y
![]() 1
...(ii)
1
...(ii)
To draw the graph of 3x +2y > 5
Draw the straight line 3 x +2 y = 5 which passes through the points (5/3,0)
and (0,5/2)
The line divides the plane into two parts.
Further, as O (0, 0) does not satisfy the inequation 3 x +2 y > 5 (as 3.0 +2.0
= 0 < 5), therefore, the graph of (i) consists of that part of the plane
divided by the line 3 x +2 y = 5 which does not contain the origin.
Similarly, draw the graph of the inequation x +y ![]() 1.Shade
the common part of the graphs of both the given inequations (i) and (ii).
1.Shade
the common part of the graphs of both the given inequations (i) and (ii).
The solution set of the given inequations consists of all points in the shaded
part of the co-ordinate plane shown in fig. The points on the part EC of the
line DC are included in the solution.
Solve the following inequations simultaneously:
3 y -2 x < 4, x +3 y > 3 and x +y ![]() 5.
5.
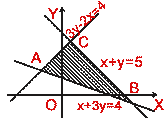
The given inequations are
3 y -2 x < 4 ...(i)
x +3 y > 3 ...(ii)
and x +y ![]() 5 ...(iii)
5 ...(iii)
To draw the graph of 3 y -2 x < 4.
Draw the straight line 3 y -2 x = 4 which passes through the points (-2, 0)
and (0,4/3). The line divides the plane into two parts.
Further as O (0, 0) satisfies the inequation 3 y -2 x < 4 (as 3.0 -2.0 =
0 < 4), therefore, the graph consists of that part of the plane divided by the
line 3 y -2 x = 4 which contains the origin.
Similarly, draw the graphs of other two inequations x +3y > 3 and x +y
![]() 5.
5.
Shade the common part of the graphs of all the three given inequations (i), (ii) and (iii).
The solution set consists of all the points in the shaded part of the
co-ordinate plane shown in fig. The points on the line segment BC are included in the solution.
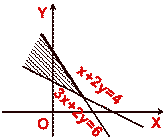
Solve the following systems of linear inequations simultaneously:
1.  2.
2. 
3. 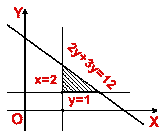 4.
4. 
5. 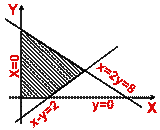 6.
6.