Slope of a Straight Line
Slope (or gradient) of a straight line
If  (
( 90°) is the inclination of a
straight line, then tan
90°) is the inclination of a
straight line, then tan  is called its slope (or
gradient). The slope of a line is usually denoted by m.
is called its slope (or
gradient). The slope of a line is usually denoted by m.
Remark. Since tan  is not defined when
is not defined when
 = 90°, therefore, the slope of a vertical line is not
defined.
= 90°, therefore, the slope of a vertical line is not
defined.
Slope of the line joining two points
The slope m of a non-vertical line passing through the points P(x1
, y1) and Q(x1, y1) is given by
slope = m = (y2 -y1)/(x2
-x1)
Remarks
- Two (non-vertical) lines are parallel iff their slopes are equal.
- Two (non-vertical) lines are perpendicular iff the product of their slopes = -1.
- Slope of a perpendicular line is the negative reciprocal of the slope of the given line.
Illustrative Examples
Example
Without using Pythagoras theorem, show that the points A (1, 2), B (4, 5)
and C (6, 3) are the vertices of a right-angled triangle.
Solution
In  ABC, we have
ABC, we have
m1 = slope of AB = (5 -2)/(4-1) = 3/3 = 1 and
m2 = slope of BC = (3 -5)/(6-4) = 2/2 = -1
m1 m2 = 1. (-1) = -1 => AB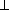 BC
BC
Hence, the given points are the vertices of a right-angled triangle.
Example
Using slopes, show that the points A (6, -1), B (5, 0) and C (2, 3) are collinear.
Solution
Slope of AB = [0 -(-1)]/(5-6) = 1/(-1) = -1
and slope of AC = [3 -(-1)]/(2-6) = 4/(-4) = -1
=> slope of AB = slope of AC
=> AB and AC are parallel.
But AB and AC have point A is common, therefore, the given points A, B and C are collinear.
Exercise
- Find the slope of a line whose inclination is:
(i) 30°
(ii) 2  /3
(iii)
/3
(iii)  /3
/3
- Find the inclination of a line whose gradient is:
(i) 1/  3
(ii) -1
(iii) -
3
(ii) -1
(iii) -  3
3
- Find the gradient of the line containing the points
(i) (-2, 3) and (5, -7)
(ii) (3, -7) and (0, 2)
- A line passes through the points (4, -6) and (-2, -5). Does it make an
acute angle with the positive direction of x-axis?
- Find the equation of the locus of all points P such that the slope of the
line joining origin and P is - 2.
- Show that the line joining (2, -3) and (-5, 1) is
(i) parallel to the line joining (7, -1) and (0, 3)
(ii) perpendicular to the line joining (4, 5) and (0, - 2)
- State, whether the two lines in each of the following problems are
parallel, perpendicular or neither:
(i) through (2, -5) and (-2, 5); through (6, 3) and (1, 1)
(ii) through (5, 6) and (2, 3); through (9, -2) and (6, - 5)
(iii) through (8, 2) and (-5, 3); through (16, 6) and (3, 15)
- Find y if the slope of the line joining (-8, 11), (2, y) is - 4/3.
- Find the value of x so that the line through (x, 9) and (2, 7) is
parallel to the line through (2, - 2) and (6, 4).
- Without using Pythagoras theorem, show that the points (4, 4), (3, 5) and
(-1, -1) are the vertices of a right angled triangle.
Answers
1. (i) 1/  3
(ii) -
3
(ii) -  3
(iii) not defined
3
(iii) not defined
2. (i) 30°
(ii) 135°
(iii) 120°
3. (i)- 10/7
(ii) -3
4. No
5. 2x +y = 0
7. (i) Perpendicular
(ii) parallel
(iii) neither
8. -7/3
9. 10./3
![]() (
(![]() 90°) is the inclination of a
straight line, then tan
90°) is the inclination of a
straight line, then tan ![]() is called its slope (or
gradient). The slope of a line is usually denoted by m.
is called its slope (or
gradient). The slope of a line is usually denoted by m.![]() is not defined when
is not defined when
![]() = 90°, therefore, the slope of a vertical line is not
defined.
= 90°, therefore, the slope of a vertical line is not
defined.![]() ABC, we have
ABC, we have![]() BC
BC