sin A = 2
The three angles and the three sides of a triangle are called the six elements of the triangle. If three elements of a triangle are given (at least one of them being a side), the other three can be found out by using sine rule, law of cosines and / or semi-sum formulae. This process of finding the unknown elements is called solving a triangle.
If we know the two sides and one angle (i.e. 90°), we can use Pythagoras theorem to find the third side and then the sine rule to find other two angles.
If one side and another angle are known, we can find the third angle from A +B +C =180°, and then use sine rule to find the other two sides.
We categorise such cases in four categories:
(i) When three sides are given. (SSS)
(ii) When two sides and the included angle are given. (SAS)
(iii) When one side and two angles are given. (SAA)
(iv) When two sides and an angle opposite to one of them are given. (SSA)
(1) When three sides are given (SSS)
As a, b, c are known, first we find the semi-perimeter s = (a +b +c)/2
Then we calculate two angles by using any of the following formulae:
![]()
![]()
![]()
sin A = 2![]() /bc, cos A = (b²+c² -a²)/2bc
/bc, cos A = (b²+c² -a²)/2bc
Then the third angle can be found by using A +B +C = 180°
(2) When two sides and the included angle are given (SAS)
Let sides b, c and angle A be given (b > c).
Then A +B +C = 180° => B +C = 180° -A
After this, we use Napier Analogy: tan (B -C)/2 = [(b -c)/(b+c)]cot A/2
From this (B -C)/2 and thus, B -C can be found.
Now, since B +C and B -C are known, we can find B and C by adding and
subtracting. The side a can be found by using sine rule.
(3) When one side and two angles are given (SAA)
We can find the third angle using A +B +C = 180°. Then we calculate the other two sides using sine rule.
(4) When two sides and an angle opposite to one of them is given (SSA)
Let the two side b, c be given, and also angle B (opposite to given side b) be given.
To find angle c, we use sine rule:
b/sin B = c/sin C
=> sin C = c sin B/b
Three cases arise:
(i) If c sin B > b, then sin C > 1, which is not possible. Hence there is
no solution.
(ii) If c sin B = b, we get sin C = 1 => C = 90°. Then the triangle can
be solved.
(iii) If c sin B < b, then sin C < 1, and two values of C are possible, say C1
(0 < C1 < 90°) and C2 = 180° -C1 (90° < C2
< 180°). If B +C2 < 180°, two solutions of given triangle are
possible, and this is called ambiguous case. If B +C2 >
180°, we have to reject this value of C (i.e. C2) and solve the
triangle by using value C1 only.
Solve the right angled triangle where
(i) ![]() C = 90°,
C = 90°,
![]() A = 30° and c = 10
A = 30° and c = 10
(ii) ![]() A = 90°,
A = 90°,
![]() C = 56° and a = 50.
C = 56° and a = 50.


Solve the ![]() ABC, if a = 24·2, b = 37·5, c
= 28·9.
ABC, if a = 24·2, b = 37·5, c
= 28·9.
2 s = a +b +c = 24·2 +37·5 +28·9 = 90· 6 => s
= 45·3
s -a = 21·1, s -b = 7·8, s -c = 16· 4
Now ![]()
log tan A/2 = (1/2) [log 7·8 +log 16·4 -log 45·3 -log 21·1]
= (1/2) [0·8921 +1·2148 -1· 6561 -1·3243]
= (1/2) [2·1069 -2·9804] = [-0·8735] = -0· 4367 = ·5633
=> A/2 = 20° 6' => A = 40° 12'
Similarly 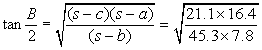
=> log tan B/2 = [log 16·4 +log 21·1 -log 45·3 -log 7·8]
= (1/2) [1·2148 +1·3243 -1·6561 -0·8921]
= (1/2) [2·5391 -2·5482] = [-0·0091] = -0·0045 = 1·9955
B/2 = 44° 42' => B = 89° 24'
Now C = 180° -(A +B) = 180° -(40° 12' +89° 24') = 180° -129° 36' = 50° 24'
Hence A = 40° 12', B = 89° 24', C = 50° 24'.
In a triangle ABC, C = ![]() /6, =
/6, =
![]() 3 and a = 1. Find the other two angles and the side.
3 and a = 1. Find the other two angles and the side.
C = ![]() /6 = 30° => A +B = 180° -C = 180° -30°
= 150°
/6 = 30° => A +B = 180° -C = 180° -30°
= 150°
Now tan (B -A)/2 = [(b -a)/(b+a)] cot C/2 = [(![]() 3 -1)/(
3 -1)/(![]() 3
+1)]cot 15°
3
+1)]cot 15°
= [(![]() 3 -1)/(
3 -1)/(![]() 3 + 1)].[(
3 + 1)].[(![]() 3
+1)/(
3
+1)/(![]() 3 - 1)] = 1 = tan 45°
3 - 1)] = 1 = tan 45°
=> (B -A)/2 = 45° => B -A = 90°
From B +A = 150°, B -A = 90°, we get by adding
(B +A) +(B -A) = 150° +90° => 2 B = 240° => B = 120°
A = 150° -B = 150° -120° = 30°
Now a/sin A = c/sin C =>
1/sin 30° = c/sin 30° => c = 1
Hence A = 30°, B = 120°, c = 1
In a triangle, A = 30°, B = 70° and a = 10. Solve the triangle.
C = 180° -(A +B) = 180° -(30 +70°) = 80°
Now a/sin A = b/sin B = c/sin C
=> 10/sin 30° = b/sin 70° = c/sin 80°
b = 10 sin 70°/sin 30° = 2 x 10 x 0·9397 = 18·794
and c = 10 sin 80°/sin 30° = 2 x 10 x 0·9848 = 19· 696
Solve the triangle ABC when b = 7, c = 10, B = 51°.
Using sine formula, sin C/c sin B/b => sin C = c sin B/b
log sin C = log c -log b +log sin B
= log 10 -log 7 +log sin 51°
= 1 -0·8451 +1·8905
= 0· 0454, which is +ve
=> sin C > 1, which is impossible.
Thus there is no solution.
Solve the following triangles (1 -8):