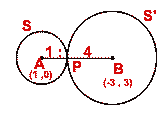
Let S, S' be two (non-concentric) circles with centers A, B and radii r1
, r2 and d be the distance between their centers, then
(i) One circle lies completely inside the other iff d < | r1 -r2
|
(ii) The two circles touch internally iff d = | r1 -r2 |
(iii) The two circles intersect in two points iff d > |r1 -r2|
and d < r1 +r2
(iv) The two circles touch externally iff d = r1 +r2
(v) One circle lies completely outside the other iff d > r1
+r2
Show that the circles x² +y² -2 x = 0 and x² +y² +6 x
-6 y +2 = 0 touch each other. Do these circles touch externally or internally?
Find the point of contact and the common tangent.
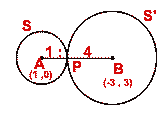
The equations of the given circles are
S = x² + y² -2 x = 0
...(i)
and S = x² + y²+6x -6y +2 = 0 ...(ii)
Their centers are A (1, 0) and B (-3, 3), and their radii are
r1 = ![]() [1² +0² -0] = 1 and r2
=
[1² +0² -0] = 1 and r2
= ![]() [9 +9 -2] = 4 respectively
[9 +9 -2] = 4 respectively
The distance between their centers
= d = ![]() [(- 3 -1)² +(3 -0)²] = 5 = 1 +4
[(- 3 -1)² +(3 -0)²] = 5 = 1 +4
=> d = r1 + r2
=> the given circles (i) and (ii) touch externally and the point of
contact P divides [AB] internally in the ratio r1 : r2
i.e. in the ratio 1 : 4
The co-ordinates of the point of contact are
(1.(-3) +4.1)/(1+4), (1.3 +4.0)/(1+4) i.e. (1/5, 3/5)
The equation of the common tangent is S -S' = 0
=> -8 x +6 y -2 = 0 => 4 x -3 y +1 = 0